What Is The Maximum Vertical Distance Between The Line - The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. The distance=|x2 − x − 30| | x 2 − x − 30 |. What is the maximum vertical distance between the line y = x + 20 and the. Find the value of x x which maximizes this using the. The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy.
The distance=|x2 − x − 30| | x 2 − x − 30 |. The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 and the. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. Find the value of x x which maximizes this using the. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy.
To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. What is the maximum vertical distance between the line y = x + 20 and the. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The distance=|x2 − x − 30| | x 2 − x − 30 |. The maximum distance is 4289 and can be found at x = 21. Find the value of x x which maximizes this using the. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1.
Solved What is the maximum vertical distance between the line y=x+30
The distance=|x2 − x − 30| | x 2 − x − 30 |. Find the value of x x which maximizes this using the. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. What is the maximum.
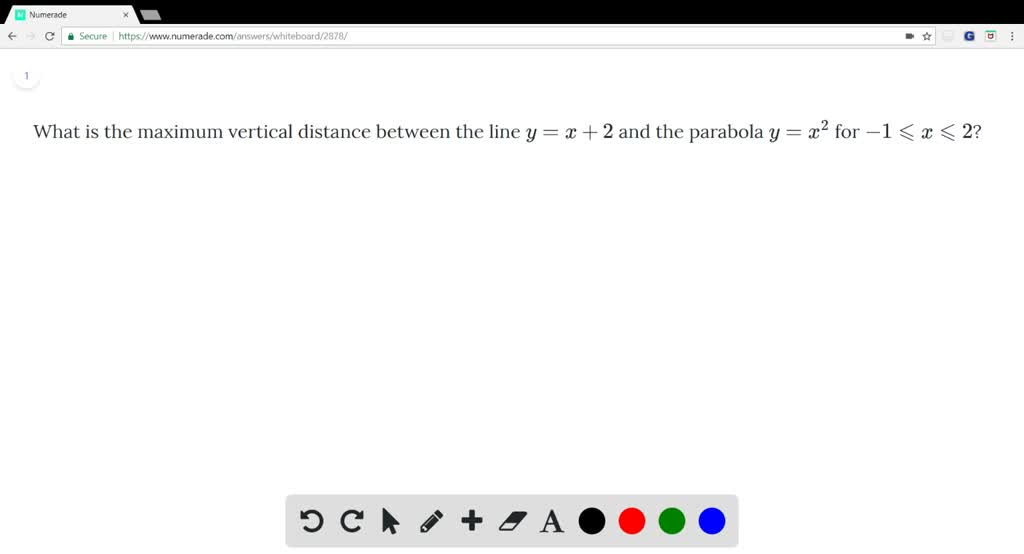
What is the Maximum Vertical Distance Between Y=X+2 and Y=X^2
The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 y =.
What is the maximum vertical distance between the line y=x+ Quizlet
The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The distance=|x2 − x − 30| | x 2 − x − 30.
SOLVEDWhat is the maximum vertical distance between the line y=x+2 and
What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The distance=|x2 − x − 30| | x 2 − x − 30 |. What is the maximum vertical distance between the line y = x + 20 and the. The maximum distance is 4289 and can.
SOLVED What is the maximum vertical distance between the line y = x
What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. Find the value of x x which maximizes this using the. The distance=|x2 − x − 30| | x 2 − x − 30 |. To find the maximum vertical distance, we need to find the maximum.
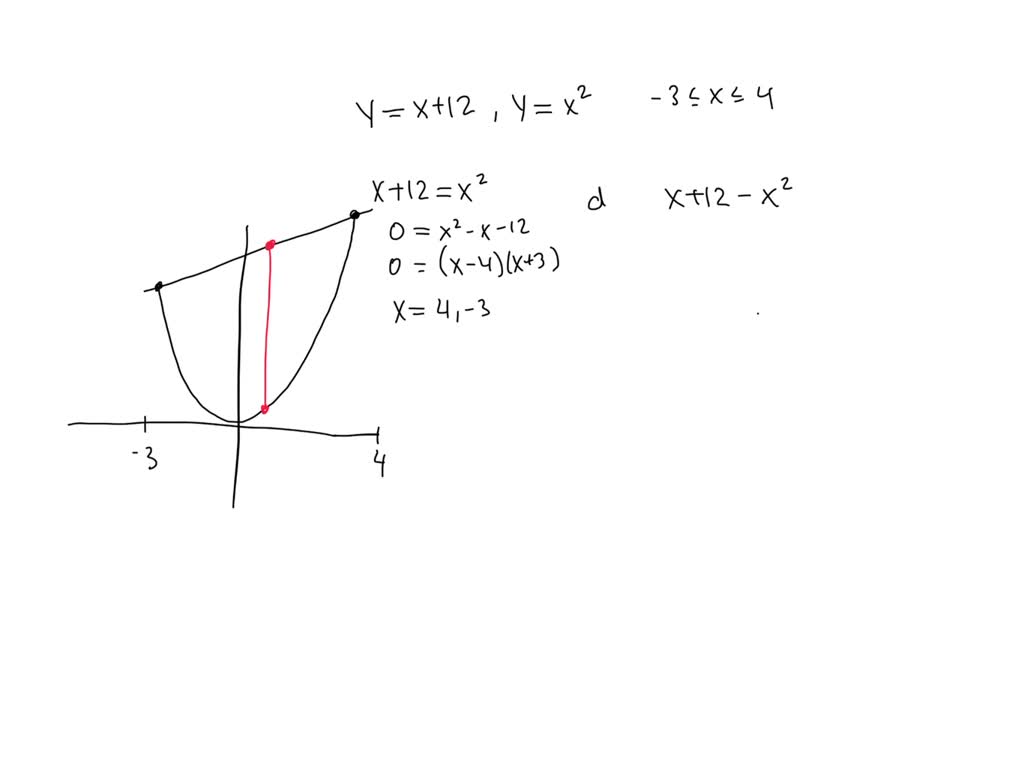
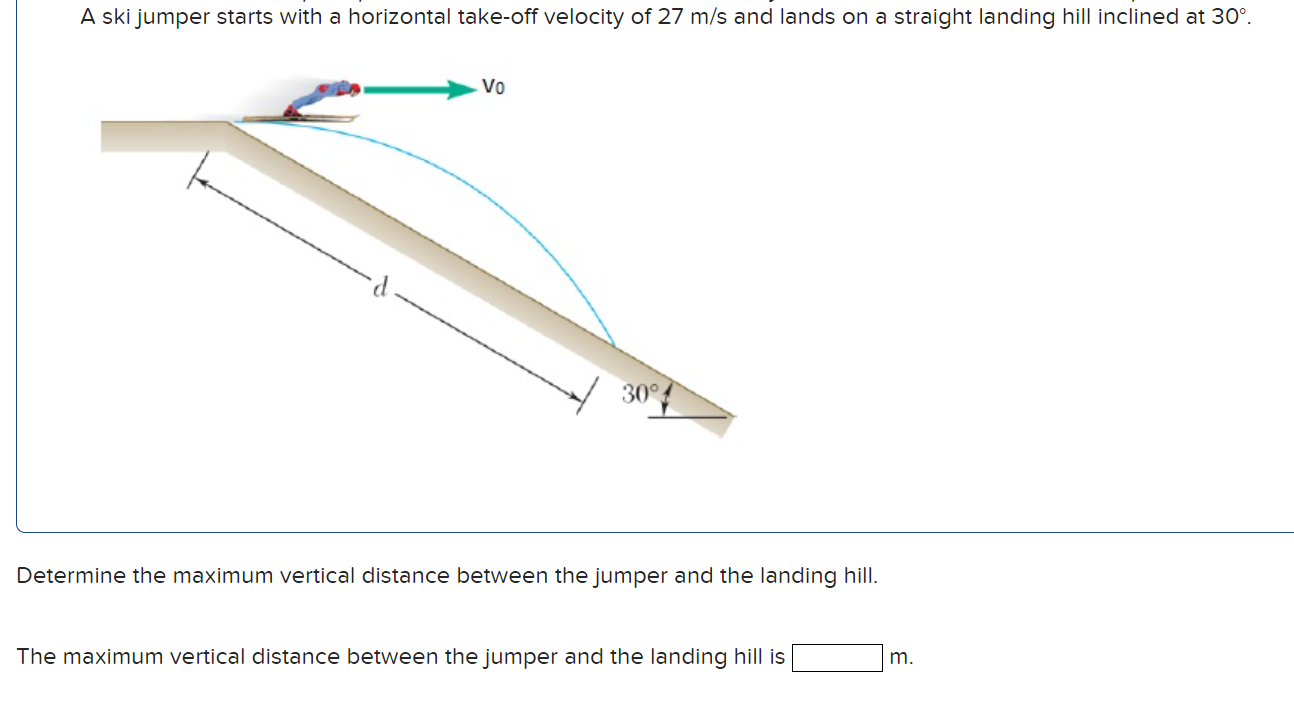
Solved Determine the maximum vertical distance between the
To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The maximum distance is 4289 and can be found at x = 21. The derivative of g(x) g (x), g′(x) =.
What is the Maximum Vertical Distance Between Y=X+2 and Y=X^2
Find the value of x x which maximizes this using the. The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 and the. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of.
SOLVED Optimization What is the maximum vertical distance between
The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The distance=|x2 − x − 30|.
Solved What is the maximum vertical distance between the line y=x+2
The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x).
[Solved] What is the maximum vertical distance between the line y = x
The distance=|x2 − x − 30| | x 2 − x − 30 |. Find the value of x x which maximizes this using the. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The maximum distance is 4289 and can be found at x =.
What Is The Maximum Vertical Distance Between The Line Y = X + 20 And The.
What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The maximum distance is 4289 and can be found at x = 21. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. The distance=|x2 − x − 30| | x 2 − x − 30 |.
Find The Value Of X X Which Maximizes This Using The.
To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy.