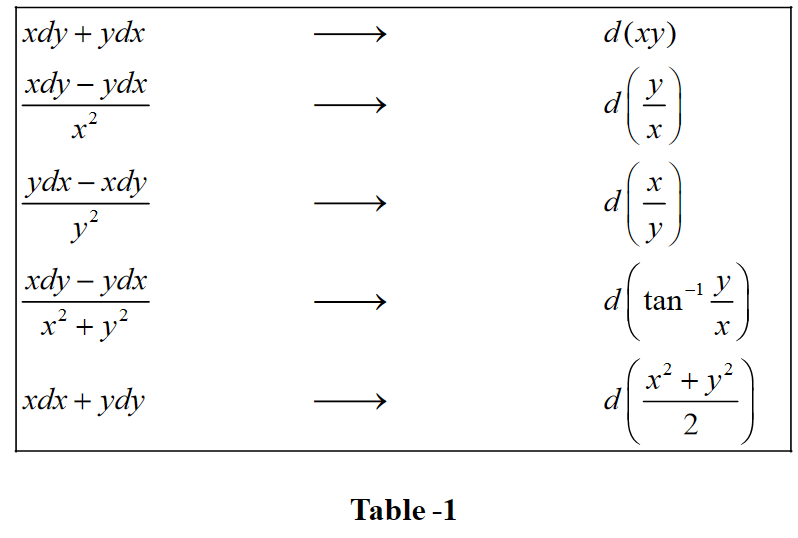
Exact Differential - Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,.
Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,.
Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,.
LECTURE 5 Exact Differential Equations PDF Equations Fair Use
Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,. Learn the.
Exact differential equation Alchetron, the free social encyclopedia
We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,. Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. Learn how to identify and solve exact differential equations of.
Exact differential equations Yawin
Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,. Learn the.
Examples On Exact Differential Equations What is Examples On Exact
Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,. Learn how to identify and solve exact differential equations of.
Engineering Mathematics Reducible to Exact Differential equation
Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. We call the differential m dx+n dy exact, in a region d where m.
Exact differential equations
We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,. Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. Learn the.
Exact Differential Equations Differential Equations Equations
We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,. Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. Learn how to identify and solve exact differential equations of.
Exact Differential Equation PDF
Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. We call the differential m dx+n dy exact, in a region d where m.
Engineering Mathematics Reducible to Exact Differential equation
We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,. Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. Learn the.
[Solved] Exact differential equations a. Show that any differential
Learn the definitions and properties of exact and inexact differentials, and how to apply them in thermodynamics and calculus. We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,. Learn how to identify and solve exact differential equations of.
Learn The Definitions And Properties Of Exact And Inexact Differentials, And How To Apply Them In Thermodynamics And Calculus.
Learn how to identify and solve exact differential equations of the form m(x, y) dx + n(x, y) dy = 0 by finding a potential function φ. We call the differential m dx+n dy exact, in a region d where m and n are defined, if it is the total differential of some function f(x,y) in this region,.