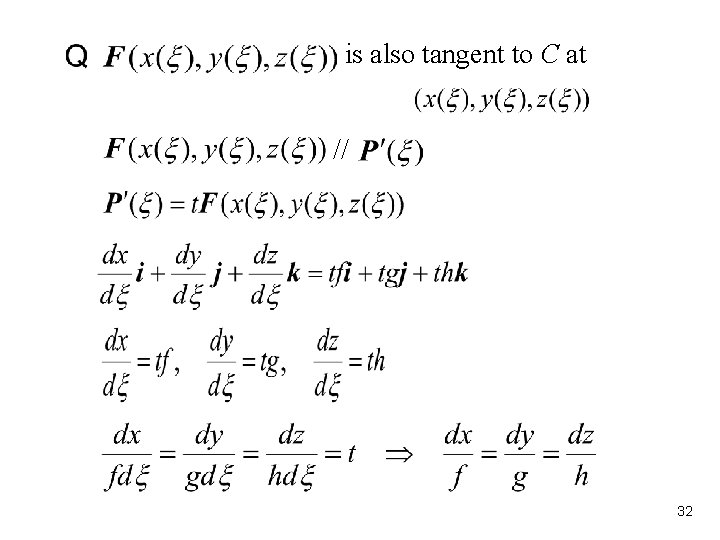Vector Differential - The derivative of a vector can be interpreted geometrically as shown in fig. F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. It is used to define the gradient , divergence ∙, curl ×, and. A good example of a vector field is. U is the increment in u consequent upon an increment t. Technically, by itself is neither a vector nor an operator, although it acts like both.
A good example of a vector field is. The derivative of a vector can be interpreted geometrically as shown in fig. U is the increment in u consequent upon an increment t. It is used to define the gradient , divergence ∙, curl ×, and. F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. Technically, by itself is neither a vector nor an operator, although it acts like both.
F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. Technically, by itself is neither a vector nor an operator, although it acts like both. A good example of a vector field is. U is the increment in u consequent upon an increment t. It is used to define the gradient , divergence ∙, curl ×, and. The derivative of a vector can be interpreted geometrically as shown in fig.
Differential Vector Solid Icons. Simple stock illustration stock
It is used to define the gradient , divergence ∙, curl ×, and. The derivative of a vector can be interpreted geometrically as shown in fig. F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. A good example of a vector field is. Technically, by itself is neither a vector nor.
Supplemental VectorValued Differential Forms CS 15458/858
F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. The derivative of a vector can be interpreted geometrically as shown in fig. It is used to define the gradient , divergence ∙, curl ×, and. A good example of a vector field is. U is the increment in u consequent upon.
Differential Vector Outline Icons. Simple stock illustration stock
The derivative of a vector can be interpreted geometrically as shown in fig. It is used to define the gradient , divergence ∙, curl ×, and. A good example of a vector field is. Technically, by itself is neither a vector nor an operator, although it acts like both. U is the increment in u consequent upon an increment t.
(PDF) Applications of Vector differential operator del
A good example of a vector field is. F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. U is the increment in u consequent upon an increment t. Technically, by itself is neither a vector nor an operator, although it acts like both. It is used to define the gradient ,.
Differential Gear Stock Vector 258490832 Shutterstock
It is used to define the gradient , divergence ∙, curl ×, and. Technically, by itself is neither a vector nor an operator, although it acts like both. A good example of a vector field is. U is the increment in u consequent upon an increment t. F(x,y,z)) is often represented by drawing the vector f(r) at point r for.
Chapter 9 Vector Differential Calculus 9 1 Vector
F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. A good example of a vector field is. Technically, by itself is neither a vector nor an operator, although it acts like both. It is used to define the gradient , divergence ∙, curl ×, and. The derivative of a vector can.
Differential Royalty Free Vector Image VectorStock
It is used to define the gradient , divergence ∙, curl ×, and. A good example of a vector field is. F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. The derivative of a vector can be interpreted geometrically as shown in fig. U is the increment in u consequent upon.
Chapter 9 Vector Differential Calculus 9 1 Vector
Technically, by itself is neither a vector nor an operator, although it acts like both. The derivative of a vector can be interpreted geometrically as shown in fig. It is used to define the gradient , divergence ∙, curl ×, and. A good example of a vector field is. U is the increment in u consequent upon an increment t.
Chapter 9 Vector Differential Calculus 9 1 Vector
The derivative of a vector can be interpreted geometrically as shown in fig. F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain. Technically, by itself is neither a vector nor an operator, although it acts like both. U is the increment in u consequent upon an increment t. It is used.
Understanding vector differential
U is the increment in u consequent upon an increment t. It is used to define the gradient , divergence ∙, curl ×, and. A good example of a vector field is. The derivative of a vector can be interpreted geometrically as shown in fig. Technically, by itself is neither a vector nor an operator, although it acts like both.
It Is Used To Define The Gradient , Divergence ∙, Curl ×, And.
Technically, by itself is neither a vector nor an operator, although it acts like both. A good example of a vector field is. U is the increment in u consequent upon an increment t. F(x,y,z)) is often represented by drawing the vector f(r) at point r for representative points in the domain.