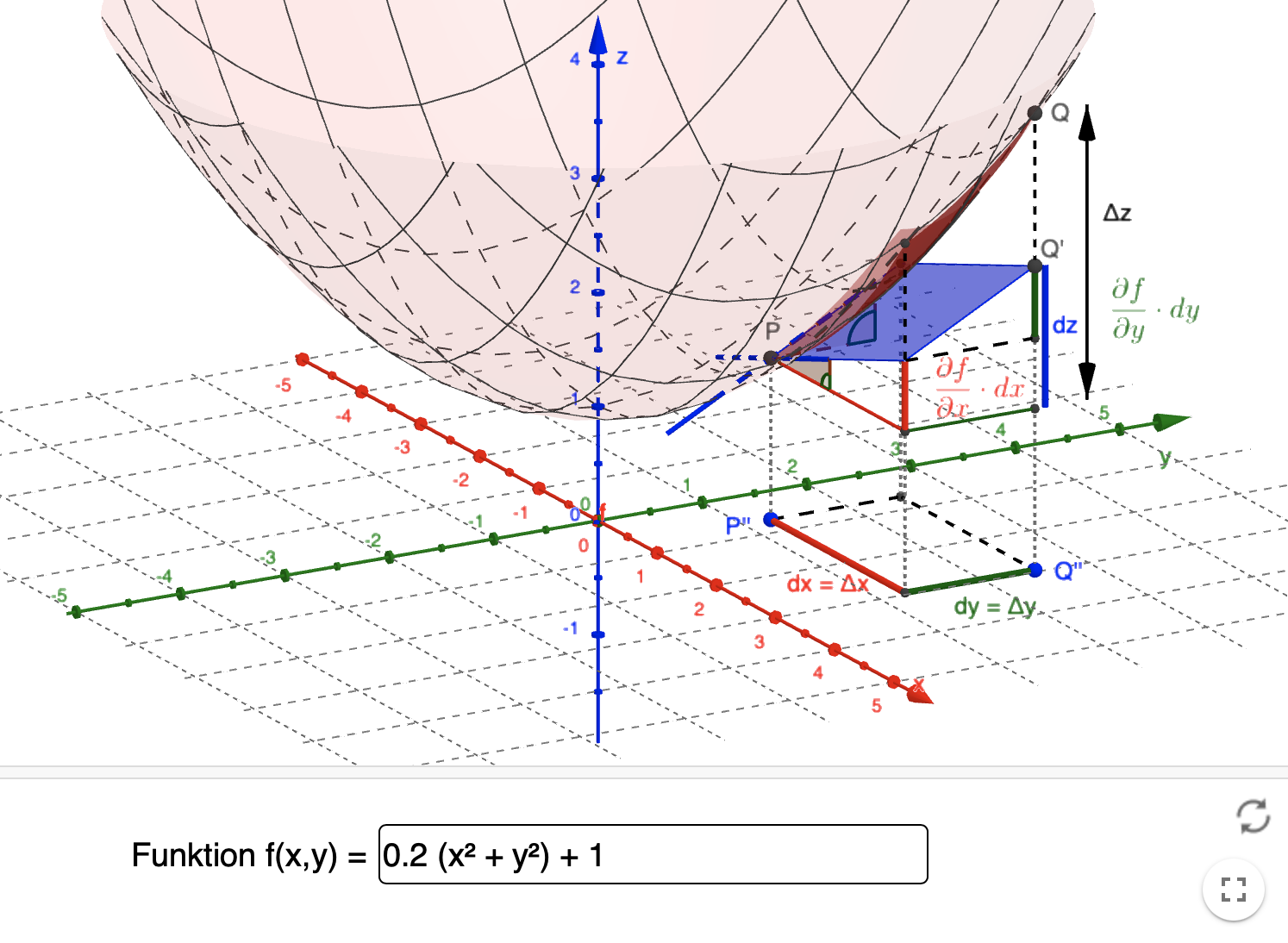
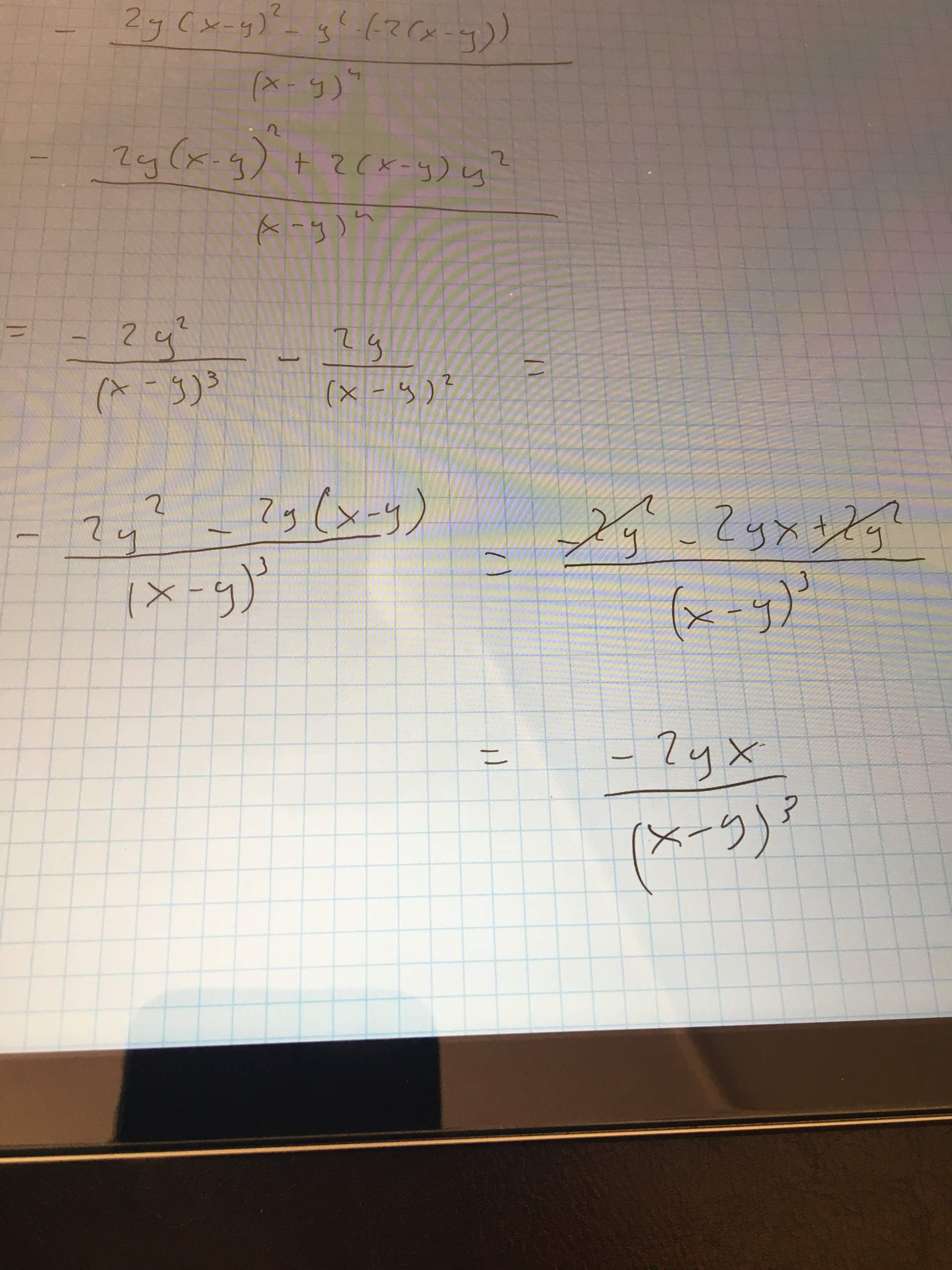Totales Differential - Total differentials can be generalized. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. For a function f = f(x, y, z) whose partial derivatives exists, the total. Let \(z=f(x,y)\) be continuous on an open set \(s\). Let \(dx\) and \(dy\) represent changes in \(x\) and. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted.
The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Total differentials can be generalized. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. Let \(z=f(x,y)\) be continuous on an open set \(s\). Let \(dx\) and \(dy\) represent changes in \(x\) and. For a function f = f(x, y, z) whose partial derivatives exists, the total.
Let \(dx\) and \(dy\) represent changes in \(x\) and. Total differentials can be generalized. Let \(z=f(x,y)\) be continuous on an open set \(s\). For a function f = f(x, y, z) whose partial derivatives exists, the total. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. F(x + ∆x, y + ∆y) = f(x, y) + ∆z.
calculus Visualizing the total differential Mathematics Stack Exchange
Total differentials can be generalized. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. For a function f = f(x, y, z) whose partial derivatives exists, the total. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted..
Lösungen von Totalen Differential Aufgaben Tipps & Tricks zur
Total differentials can be generalized. Let \(z=f(x,y)\) be continuous on an open set \(s\). Let \(dx\) and \(dy\) represent changes in \(x\) and. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. For a function f = f(x, y, z) whose partial derivatives exists, the total.
Totales Differential Mathelounge
For a function f = f(x, y, z) whose partial derivatives exists, the total. Let \(dx\) and \(dy\) represent changes in \(x\) and. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. Let \(z=f(x,y)\) be continuous on an open set \(s\). The former part of δ x is called the (total) differential or the exact differential of.
Totales Differential Aufgaben
F(x + ∆x, y + ∆y) = f(x, y) + ∆z. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Let \(z=f(x,y)\) be continuous on an open set \(s\). Let \(dx\) and \(dy\) represent changes in \(x\) and. Total.
Totales Differential Mathelounge
For a function f = f(x, y, z) whose partial derivatives exists, the total. Total differentials can be generalized. Let \(dx\) and \(dy\) represent changes in \(x\) and. Let \(z=f(x,y)\) be continuous on an open set \(s\). F(x + ∆x, y + ∆y) = f(x, y) + ∆z.
Totales Differential berechnen und prüfen? (Schule, Mathe, Mathematik)
Total differentials can be generalized. For a function f = f(x, y, z) whose partial derivatives exists, the total. Let \(z=f(x,y)\) be continuous on an open set \(s\). The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. F(x +.
Totales Differential
Let \(dx\) and \(dy\) represent changes in \(x\) and. For a function f = f(x, y, z) whose partial derivatives exists, the total. Total differentials can be generalized. Let \(z=f(x,y)\) be continuous on an open set \(s\). F(x + ∆x, y + ∆y) = f(x, y) + ∆z.
Total differential as estimation error, partial differentials as
Let \(dx\) and \(dy\) represent changes in \(x\) and. Total differentials can be generalized. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. For a function f =.
partial derivative Total differential definition help Mathematics
Let \(dx\) and \(dy\) represent changes in \(x\) and. Total differentials can be generalized. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. Let \(z=f(x,y)\) be continuous on an open set \(s\). For a function f = f(x, y, z) whose partial derivatives exists, the total.
Totales Differential MathFlix
The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. Let \(z=f(x,y)\) be continuous on an open set \(s\). Let \(dx\) and \(dy\) represent changes in \(x\) and. For.
Let \(Z=F(X,Y)\) Be Continuous On An Open Set \(S\).
Total differentials can be generalized. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. F(x + ∆x, y + ∆y) = f(x, y) + ∆z. Let \(dx\) and \(dy\) represent changes in \(x\) and.