R L Circuit Differential Equation - Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the variables and. Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze. Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Vl il r l step 1:
Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the variables and. Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze. Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Vl il r l step 1:
Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the variables and. Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze. Vl il r l step 1:
"RLC Circuit, Differential Equation Electrical Engineering Basics
Vl il r l step 1: Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the variables and. Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial.
capacitor how does the differential equation for a series RC circuit
Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the variables and. Series/parallel rlc circuits r l c i r l c v ir il r.
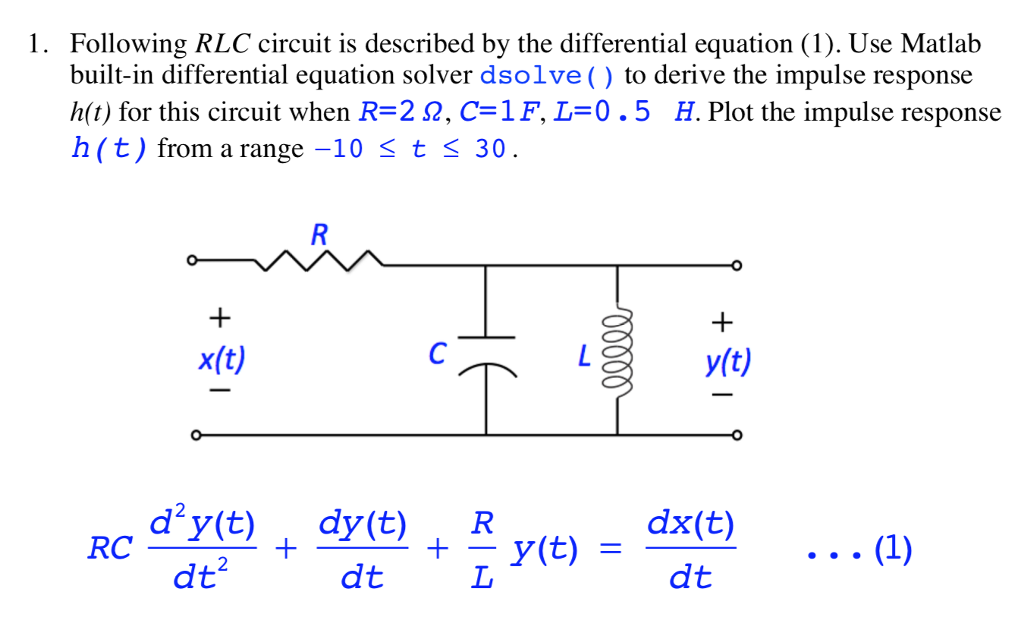
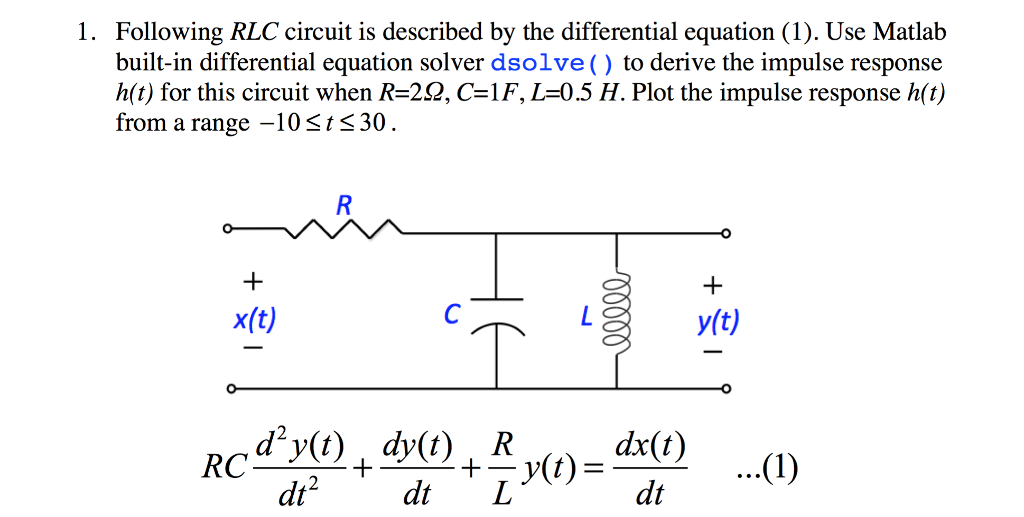
Solved 1. Following RLC circuit is described by the
Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze. Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =..
First order rc circuit differential equation
Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze..
Solved 1. Following RLC circuit is described by the
Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the variables and. Vl il r l step 1: Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Series/parallel rlc circuits r l c i r.
Differential equation for RLC circuit
Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze. Vl il r l step 1: Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the.
RL Circuit differential equation electrical engineering basi Inspire
Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the variables and. Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze. Vl il r l.
"RLC Circuit, Differential Equation Electrical Engineering Basics
Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Vl il r l step 1: Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant.
How to solve the differential equation for driven series RLC circuit?
Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Equation (0.2) is a first order homogeneous differential equation and its solution may be easily determined by separating the variables and. Series/parallel rlc circuits r l c i r l c v ir il r.
The LR series circuit differential equation acted on by an
Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze. Vl il r l step 1: Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic =.
Equation (0.2) Is A First Order Homogeneous Differential Equation And Its Solution May Be Easily Determined By Separating The Variables And.
Series/parallel rlc circuits r l c i r l c v ir il r vc v ic l i 0v * a series rlc circuit driven by a constant current source is trivial to analyze. Deriving the differential equation from the constitutive relations for a capacitor and an inductor, we can write ic = c dvc dt, and vl =. Vl il r l step 1: