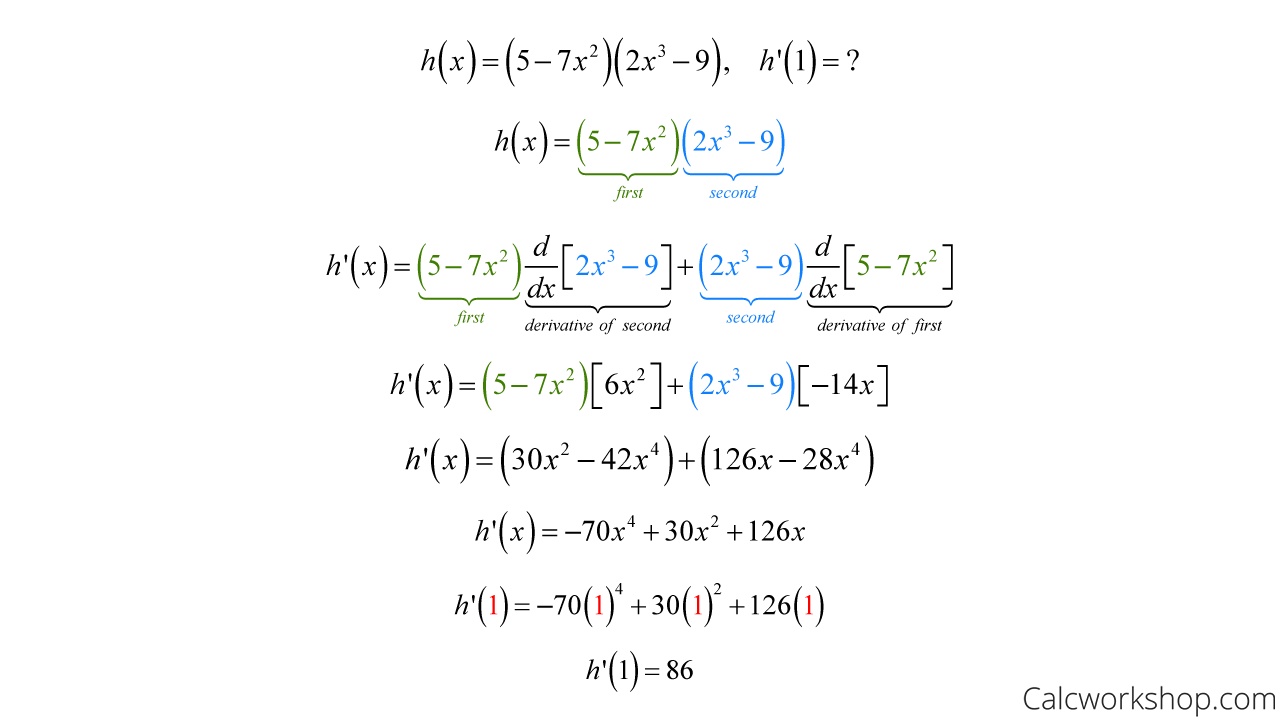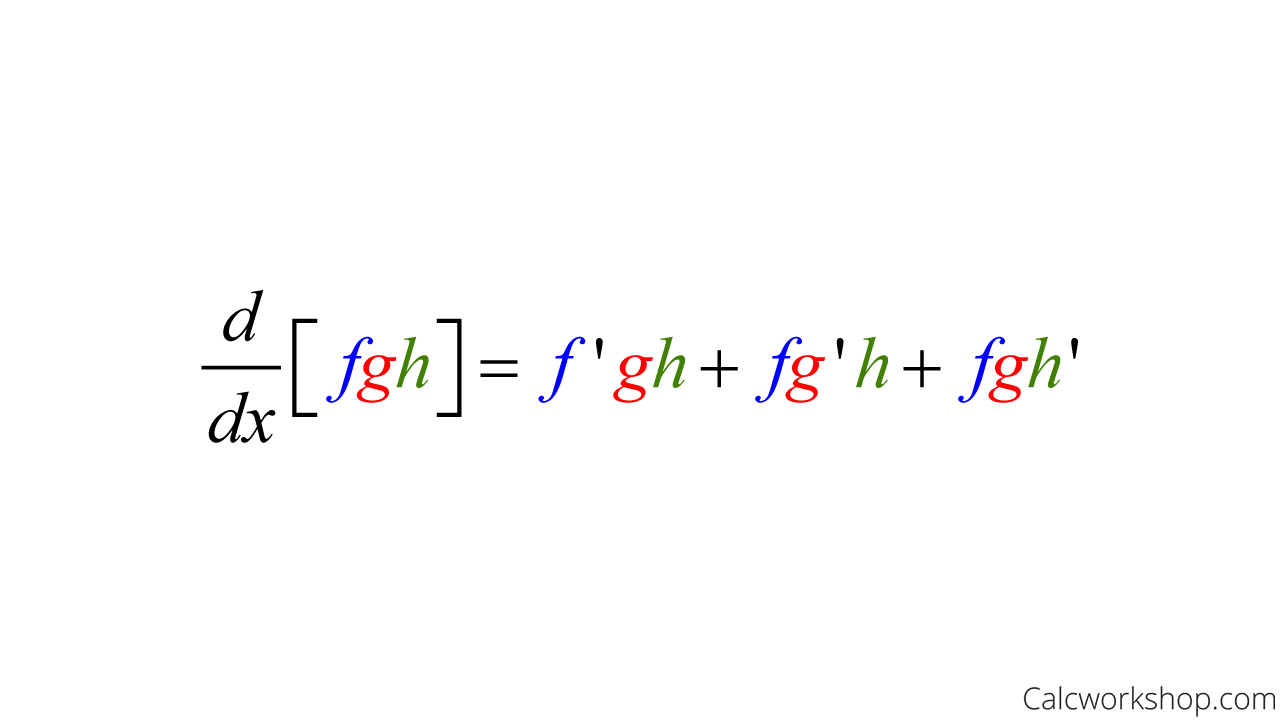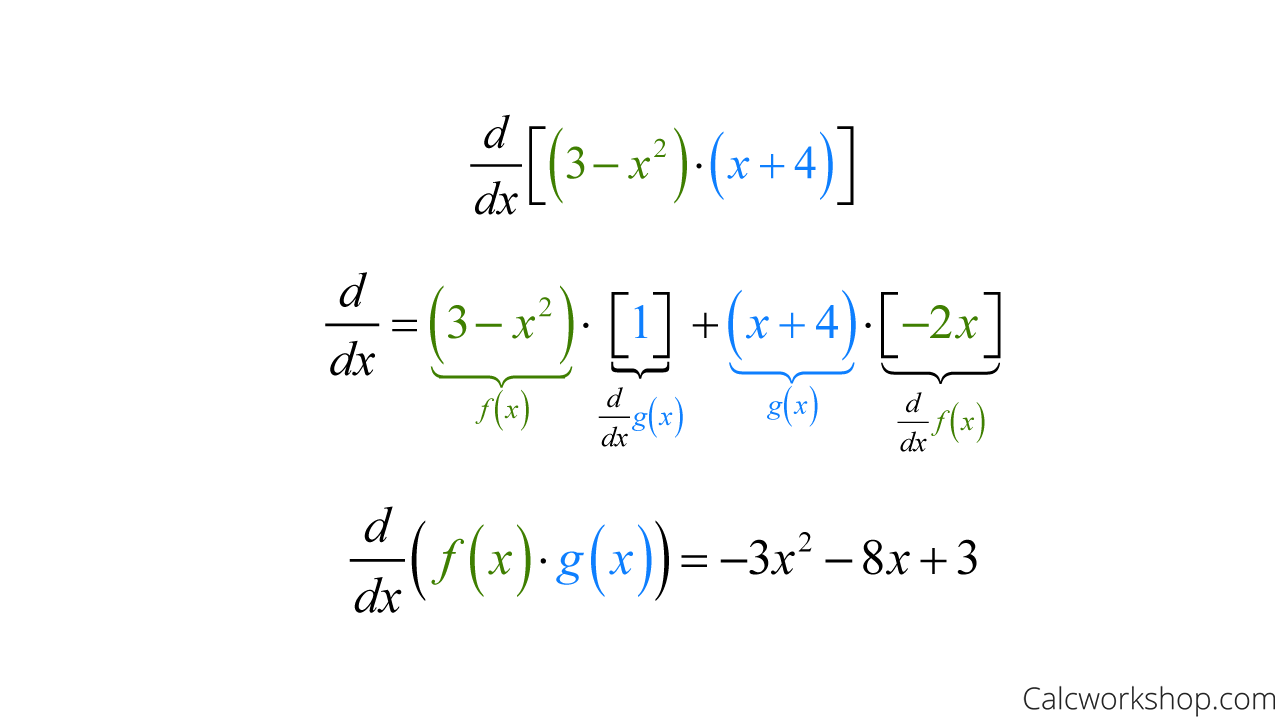Proof Of Product Rule Of Differentiation - Rewrite it in the form (because we only know. Consider the “difference quotient” i.e. All we need to do is use the definition of the derivative alongside a simple algebraic trick. Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. Steps of the proof of product rule 1. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. The product rule is a common rule for the differentiating problems where one function is multiplied by another function. ( +ℎ) ( +ℎ)− ( ) ( ) ℎ 2. It follows from the definition of derivative that if j j and k k are both differentiable on the interval i i, then: How i do i prove the product rule for derivatives?
\({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. ( +ℎ) ( +ℎ)− ( ) ( ) ℎ 2. It follows from the definition of derivative that if j j and k k are both differentiable on the interval i i, then: How i do i prove the product rule for derivatives? Rewrite it in the form (because we only know. The product rule is a common rule for the differentiating problems where one function is multiplied by another function. Steps of the proof of product rule 1. Consider the “difference quotient” i.e. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. All we need to do is use the definition of the derivative alongside a simple algebraic trick.
Rewrite it in the form (because we only know. How i do i prove the product rule for derivatives? \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. Steps of the proof of product rule 1. It follows from the definition of derivative that if j j and k k are both differentiable on the interval i i, then: Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. Consider the “difference quotient” i.e. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. The product rule is a common rule for the differentiating problems where one function is multiplied by another function. All we need to do is use the definition of the derivative alongside a simple algebraic trick.
Chain Rule Vs Product Rule
Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. How i do i prove the product rule for derivatives? Consider the “difference.
Differentiation, Product rule Teaching Resources
Consider the “difference quotient” i.e. How i do i prove the product rule for derivatives? The product rule is a common rule for the differentiating problems where one function is multiplied by another function. \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. Product rule in calculus is a.
Product Rule For Calculus (w/ StepbyStep Examples!)
Consider the “difference quotient” i.e. Rewrite it in the form (because we only know. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. Product rule in calculus is a method to find the derivative or differentiation of a function given in the form.
Proof Differentiation PDF
( +ℎ) ( +ℎ)− ( ) ( ) ℎ 2. The product rule is a common rule for the differentiating problems where one function is multiplied by another function. Rewrite it in the form (because we only know. \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved. All we.
Animated proof of the product rule Download Scientific Diagram
Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. It follows from the definition of derivative that if j j and k k are both differentiable on the interval i i, then: Rewrite it in the form (because we only know. In.
Product Rule For Calculus (w/ StepbyStep Examples!)
How i do i prove the product rule for derivatives? Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two. Rewrite it in the form (because we only know. It follows from the definition of derivative that if j j and k k.
How to differentiate a product of two functions Basic Algebra
It follows from the definition of derivative that if j j and k k are both differentiable on the interval i i, then: Steps of the proof of product rule 1. All we need to do is use the definition of the derivative alongside a simple algebraic trick. ( +ℎ) ( +ℎ)− ( ) ( ) ℎ 2. In calculus,.
Proof of Product Rule of Differentiation
How i do i prove the product rule for derivatives? In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. Consider the “difference quotient” i.e. It follows from the definition of derivative that if j j and k k are both differentiable on the.
When do I use the chain rule and when do I use the product rule in
( +ℎ) ( +ℎ)− ( ) ( ) ℎ 2. All we need to do is use the definition of the derivative alongside a simple algebraic trick. Consider the “difference quotient” i.e. In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. The product.
Product Rule For Calculus (w/ StepbyStep Examples!)
In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. It follows from the definition of derivative that if j j and k k are both differentiable on the interval i i, then: Product rule in calculus is a method to find the derivative.
Rewrite It In The Form (Because We Only Know.
In calculus, the product rule (or leibniz rule[1] or leibniz product rule) is a formula used to find the derivatives of products of two or more. How i do i prove the product rule for derivatives? All we need to do is use the definition of the derivative alongside a simple algebraic trick. Product rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two.
It Follows From The Definition Of Derivative That If J J And K K Are Both Differentiable On The Interval I I, Then:
The product rule is a common rule for the differentiating problems where one function is multiplied by another function. ( +ℎ) ( +ℎ)− ( ) ( ) ℎ 2. Steps of the proof of product rule 1. \({\left( {f\,g} \right)^\prime } = f'\,g + f\,g'\) as with the power rule above, the product rule can be proved.