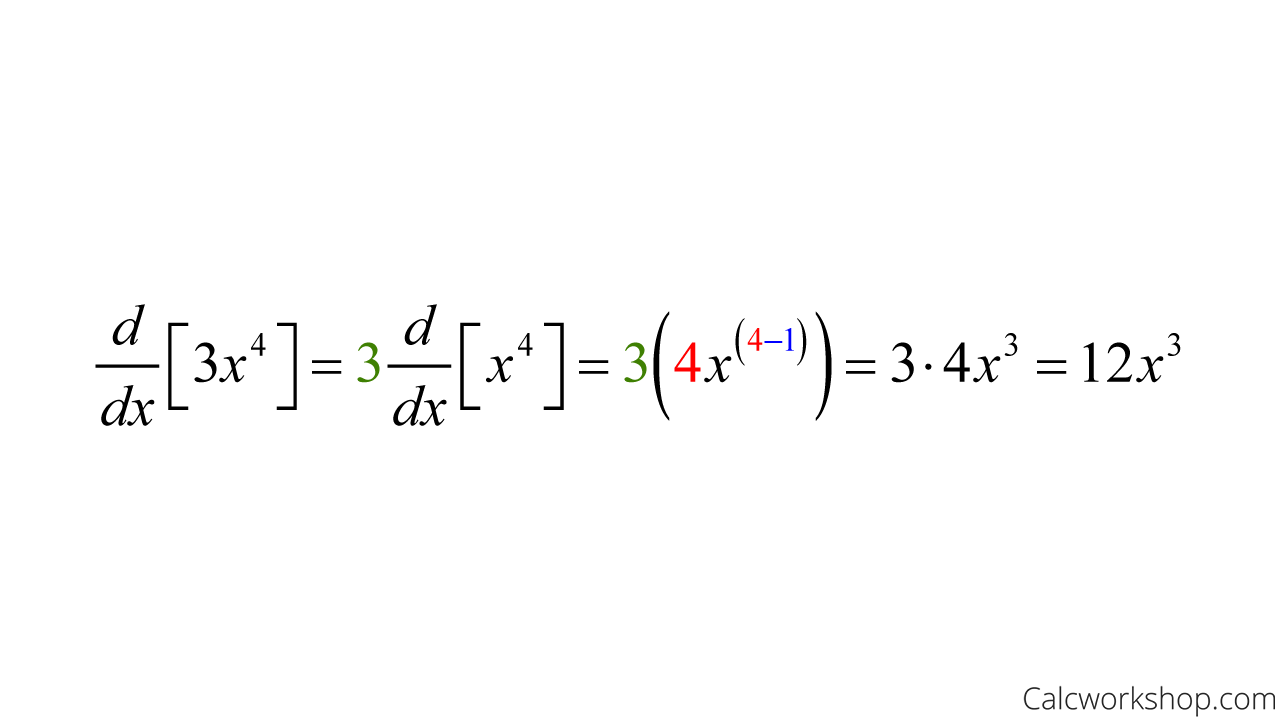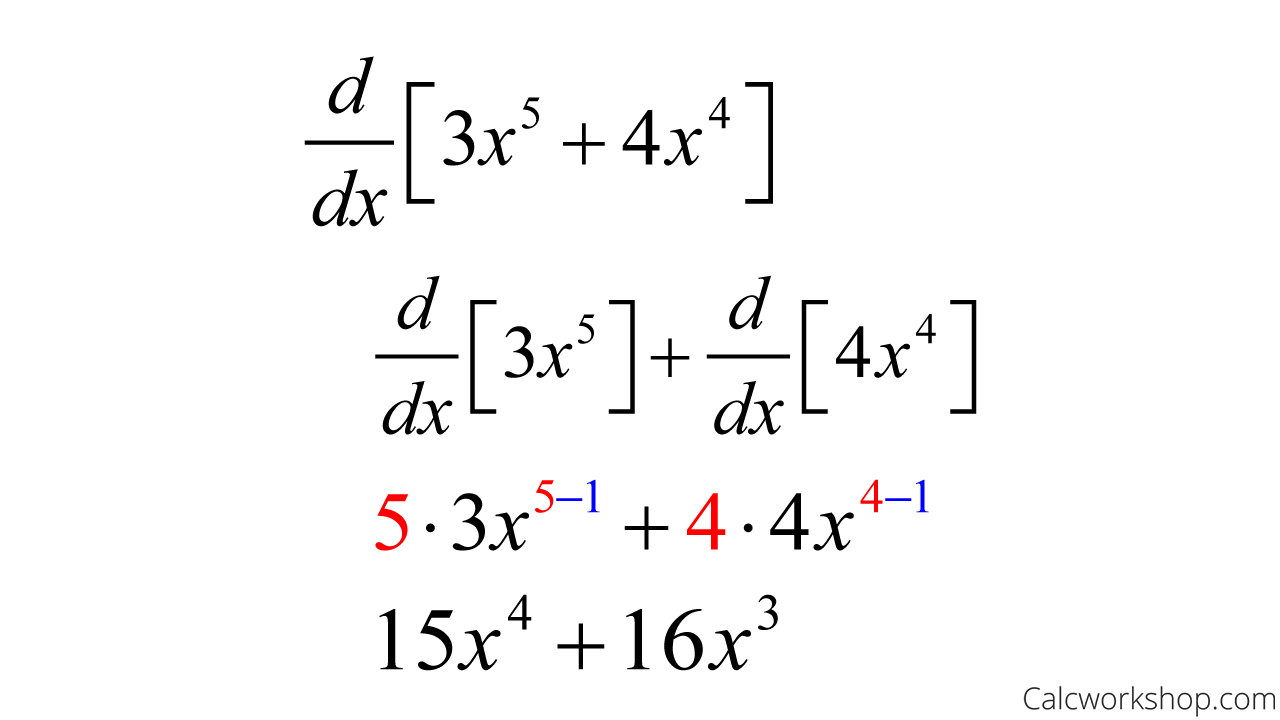Power Rule For Differentiation - The power rule is used to find the slope of polynomial functions and any other. To differentiate powers of x, we use the power rule for differentiation. Use the quotient rule for finding the derivative of a quotient of functions. This is a formula that allows. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real.
This is a formula that allows. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. Use the quotient rule for finding the derivative of a quotient of functions. The power rule is used to find the slope of polynomial functions and any other. To differentiate powers of x, we use the power rule for differentiation.
The power rule is used to find the slope of polynomial functions and any other. This is a formula that allows. To differentiate powers of x, we use the power rule for differentiation. Use the quotient rule for finding the derivative of a quotient of functions. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real.
Power Rule (How To w/ 9+ StepbyStep Examples!)
Use the quotient rule for finding the derivative of a quotient of functions. This is a formula that allows. To differentiate powers of x, we use the power rule for differentiation. The power rule is used to find the slope of polynomial functions and any other. In calculus, the power rule is used to differentiate functions of the form ().
Power Rule (How To w/ 9+ StepbyStep Examples!)
In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. This is a formula that allows. Use the quotient rule for finding the derivative of a quotient of functions. The power rule is used to find the slope of polynomial functions and any other. To differentiate powers of x, we use.
[Solved] Using the Power Rule for differentiation, find the derivatives
This is a formula that allows. To differentiate powers of x, we use the power rule for differentiation. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. The power rule is used to find the slope of polynomial functions and any other. Use the quotient rule for finding the derivative.
Power Rule (How To w/ 9+ StepbyStep Examples!)
In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. Use the quotient rule for finding the derivative of a quotient of functions. The power rule is used to find the slope of polynomial functions and any other. This is a formula that allows. To differentiate powers of x, we use.
Power Rule (How To w/ 9+ StepbyStep Examples!)
Use the quotient rule for finding the derivative of a quotient of functions. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. This is a formula that allows. To differentiate powers of x, we use the power rule for differentiation. The power rule is used to find the slope of.
[Solved] Using the Power Rule for differentiation, find the derivatives
This is a formula that allows. To differentiate powers of x, we use the power rule for differentiation. Use the quotient rule for finding the derivative of a quotient of functions. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. The power rule is used to find the slope of.
Calculus Worksheets Differentiation Rules Worksheets
The power rule is used to find the slope of polynomial functions and any other. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. This is a formula that allows. To differentiate powers of x, we use the power rule for differentiation. Use the quotient rule for finding the derivative.
A Level Maths Notes Differentiation Power Rule
This is a formula that allows. The power rule is used to find the slope of polynomial functions and any other. Use the quotient rule for finding the derivative of a quotient of functions. To differentiate powers of x, we use the power rule for differentiation. In calculus, the power rule is used to differentiate functions of the form ().
Differentiation using the power rule worksheet Portal
To differentiate powers of x, we use the power rule for differentiation. Use the quotient rule for finding the derivative of a quotient of functions. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. The power rule is used to find the slope of polynomial functions and any other. This.
A Level Maths Notes Differentiation Power Rule
The power rule is used to find the slope of polynomial functions and any other. To differentiate powers of x, we use the power rule for differentiation. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. Use the quotient rule for finding the derivative of a quotient of functions. This.
This Is A Formula That Allows.
The power rule is used to find the slope of polynomial functions and any other. Use the quotient rule for finding the derivative of a quotient of functions. In calculus, the power rule is used to differentiate functions of the form () =, whenever is a real. To differentiate powers of x, we use the power rule for differentiation.