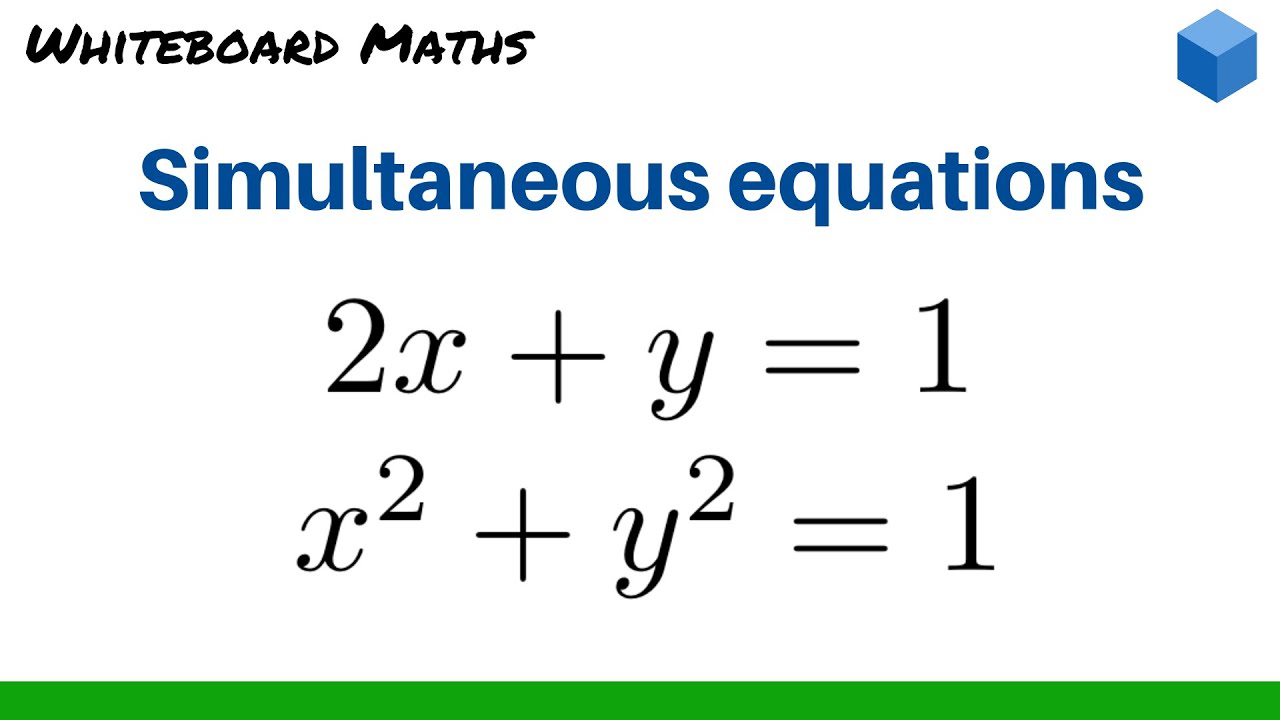Linear And Nonlinear Differential Equations Examples - Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. In a differential equation, when the variables and their derivatives are only. Differential equations are classified into linear des or nonlinear des. Linear and nonlinear differential equations are two classifications within the vast field of. The logistic equation introduces the first example of.
Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. The logistic equation introduces the first example of. Differential equations are classified into linear des or nonlinear des. Linear and nonlinear differential equations are two classifications within the vast field of. In a differential equation, when the variables and their derivatives are only.
Linear and nonlinear differential equations are two classifications within the vast field of. Differential equations are classified into linear des or nonlinear des. In a differential equation, when the variables and their derivatives are only. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. The logistic equation introduces the first example of.
Partial Differential Equations Examples
Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. The logistic equation introduces the first example of. In a differential equation, when the variables and their derivatives are only. Linear and nonlinear differential equations are two classifications within the vast field of. Differential.
And Linear Equations
Linear and nonlinear differential equations are two classifications within the vast field of. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. Differential equations are classified into linear des or nonlinear des. In a differential equation, when the variables and their derivatives are.
(PDF) Solving System of First Order Linear and Differential
The logistic equation introduces the first example of. Differential equations are classified into linear des or nonlinear des. In a differential equation, when the variables and their derivatives are only. Linear and nonlinear differential equations are two classifications within the vast field of. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after.
Second Order Differential Equations
Differential equations are classified into linear des or nonlinear des. The logistic equation introduces the first example of. Linear and nonlinear differential equations are two classifications within the vast field of. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. In a differential.
RealWorld Modeling with (Linear & Differential Equations)
Linear and nonlinear differential equations are two classifications within the vast field of. The logistic equation introduces the first example of. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. In a differential equation, when the variables and their derivatives are only. Differential.
Solved Classify each differential equations as linear or
The logistic equation introduces the first example of. Linear and nonlinear differential equations are two classifications within the vast field of. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. In a differential equation, when the variables and their derivatives are only. Differential.
Linear Versus Equations
Differential equations are classified into linear des or nonlinear des. In a differential equation, when the variables and their derivatives are only. Linear and nonlinear differential equations are two classifications within the vast field of. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | =.
SOLUTION linear and non linear differential equation examples
Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. The logistic equation introduces the first example of. In a differential equation, when the variables and their derivatives are only. Differential equations are classified into linear des or nonlinear des. Linear and nonlinear differential.
Linear Versus Equations
Linear and nonlinear differential equations are two classifications within the vast field of. The logistic equation introduces the first example of. In a differential equation, when the variables and their derivatives are only. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x. Differential.
PPT Differences Between Linear and Equations PowerPoint
Differential equations are classified into linear des or nonlinear des. In a differential equation, when the variables and their derivatives are only. Linear and nonlinear differential equations are two classifications within the vast field of. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | =.
The Logistic Equation Introduces The First Example Of.
Linear and nonlinear differential equations are two classifications within the vast field of. Differential equations are classified into linear des or nonlinear des. In a differential equation, when the variables and their derivatives are only. Using the separable method we have ∫ dy y = ∫ (1 + 1 x)dx, then after integrating we have ln | y | = x.