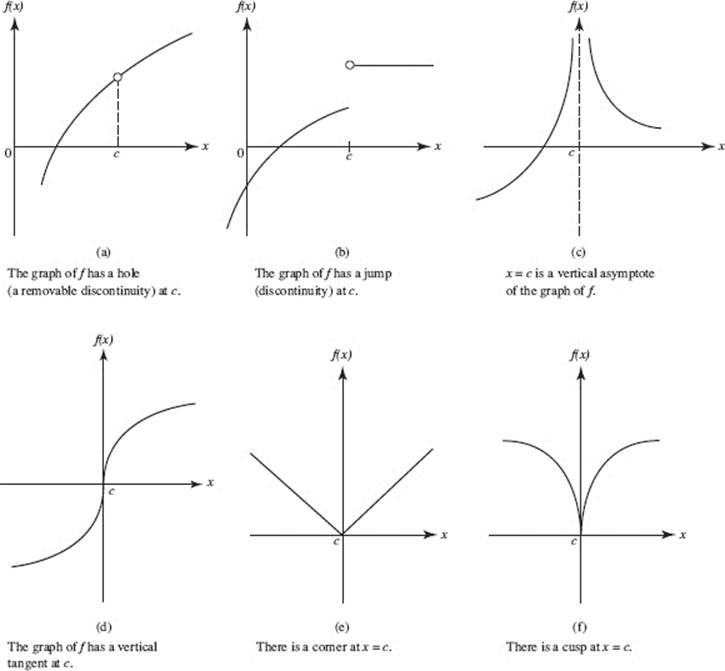
Is A Function Differentiable At A Hole - A function is not differentiable if it has a point of discontinuity in the vicinity. Two functions are identical if they have the same values on each point of their. Therefore, it is established that the function is differentiable and has a derivative at. A function is not differentiable at a point if it is. This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain. Here are three common ways:
A function is not differentiable if it has a point of discontinuity in the vicinity. Here are three common ways: A function is not differentiable at a point if it is. Therefore, it is established that the function is differentiable and has a derivative at. Two functions are identical if they have the same values on each point of their. This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain.
Therefore, it is established that the function is differentiable and has a derivative at. A function is not differentiable if it has a point of discontinuity in the vicinity. Here are three common ways: This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain. A function is not differentiable at a point if it is. Two functions are identical if they have the same values on each point of their.
Is a Function Differentiable at a Hole
This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain. Two functions are identical if they have the same values on each point of their. Therefore, it is established that the function is differentiable and has a derivative at. A function is not differentiable if it has a point of.
When Is a Function Continuous but Not Differentiable Quant RL
A function is not differentiable at a point if it is. A function is not differentiable if it has a point of discontinuity in the vicinity. Two functions are identical if they have the same values on each point of their. Therefore, it is established that the function is differentiable and has a derivative at. This function cannot have a.
Is a Function Differentiable at a Hole
Therefore, it is established that the function is differentiable and has a derivative at. This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain. A function is not differentiable if it has a point of discontinuity in the vicinity. Here are three common ways: A function is not differentiable at.
Differentiable function Wikiwand
A function is not differentiable if it has a point of discontinuity in the vicinity. This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain. Here are three common ways: A function is not differentiable at a point if it is. Two functions are identical if they have the same.
Is a Function Differentiable at a Hole
Here are three common ways: A function is not differentiable if it has a point of discontinuity in the vicinity. A function is not differentiable at a point if it is. Therefore, it is established that the function is differentiable and has a derivative at. This function cannot have a derivative at $x = 1$ because $x = 1$ is.
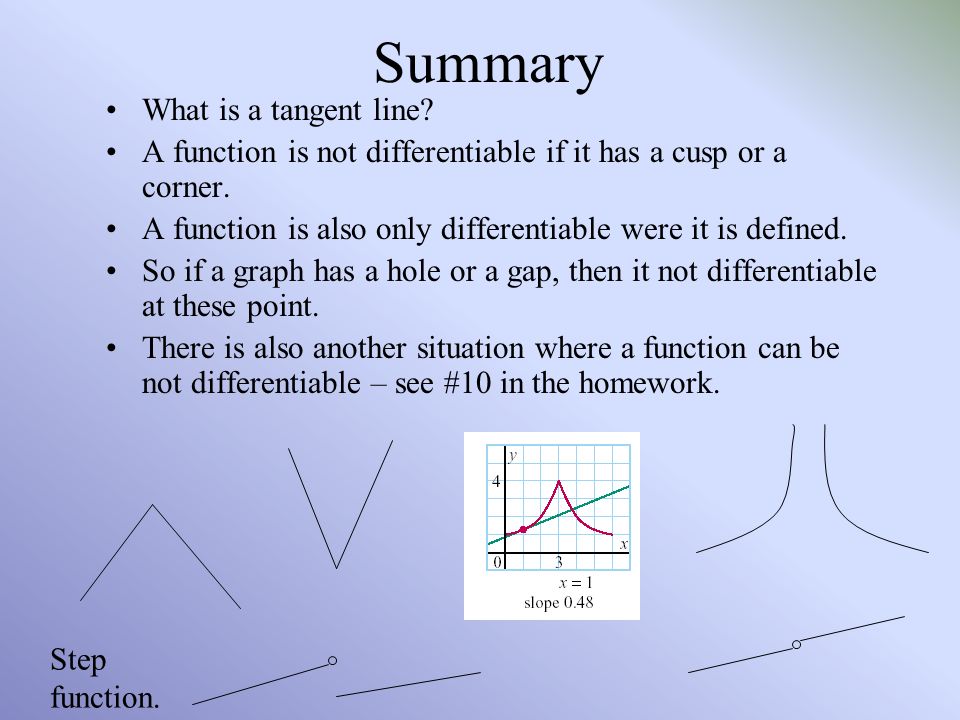
When is this function Differentiable?
Here are three common ways: A function is not differentiable at a point if it is. A function is not differentiable if it has a point of discontinuity in the vicinity. Therefore, it is established that the function is differentiable and has a derivative at. This function cannot have a derivative at $x = 1$ because $x = 1$ is.
A function differentiable along every line through
Two functions are identical if they have the same values on each point of their. Here are three common ways: This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain. Therefore, it is established that the function is differentiable and has a derivative at. A function is not differentiable if.
Is a Function Differentiable at a Hole
Therefore, it is established that the function is differentiable and has a derivative at. A function is not differentiable if it has a point of discontinuity in the vicinity. Two functions are identical if they have the same values on each point of their. Here are three common ways: A function is not differentiable at a point if it is.
Is a Function Differentiable at a Hole
Here are three common ways: A function is not differentiable if it has a point of discontinuity in the vicinity. This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain. Two functions are identical if they have the same values on each point of their. Therefore, it is established that.
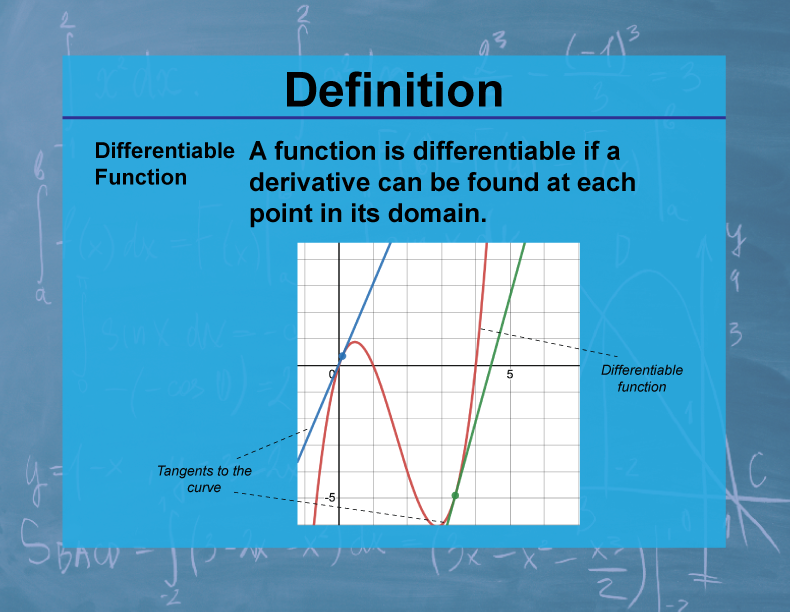
DefinitionCalculus TopicsDifferentiable Function Media4Math
A function is not differentiable at a point if it is. Two functions are identical if they have the same values on each point of their. Here are three common ways: Therefore, it is established that the function is differentiable and has a derivative at. This function cannot have a derivative at $x = 1$ because $x = 1$ is.
Two Functions Are Identical If They Have The Same Values On Each Point Of Their.
This function cannot have a derivative at $x = 1$ because $x = 1$ is not part of its domain. A function is not differentiable at a point if it is. Here are three common ways: A function is not differentiable if it has a point of discontinuity in the vicinity.