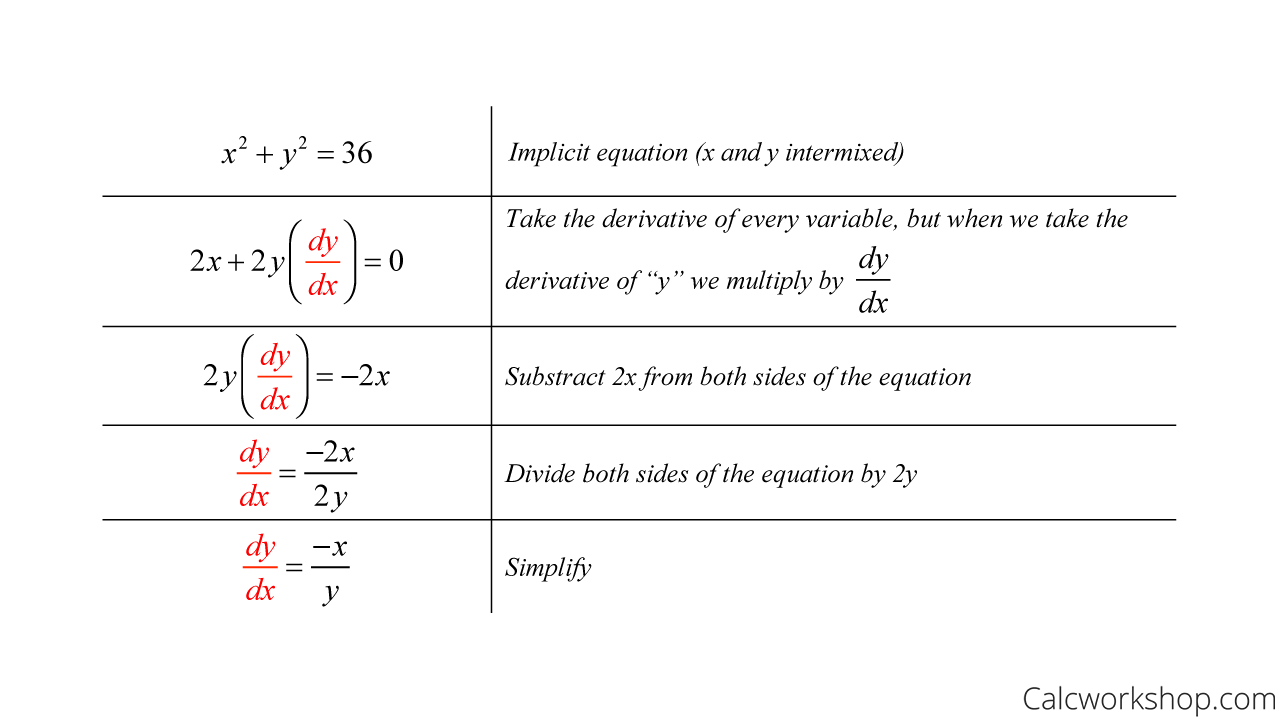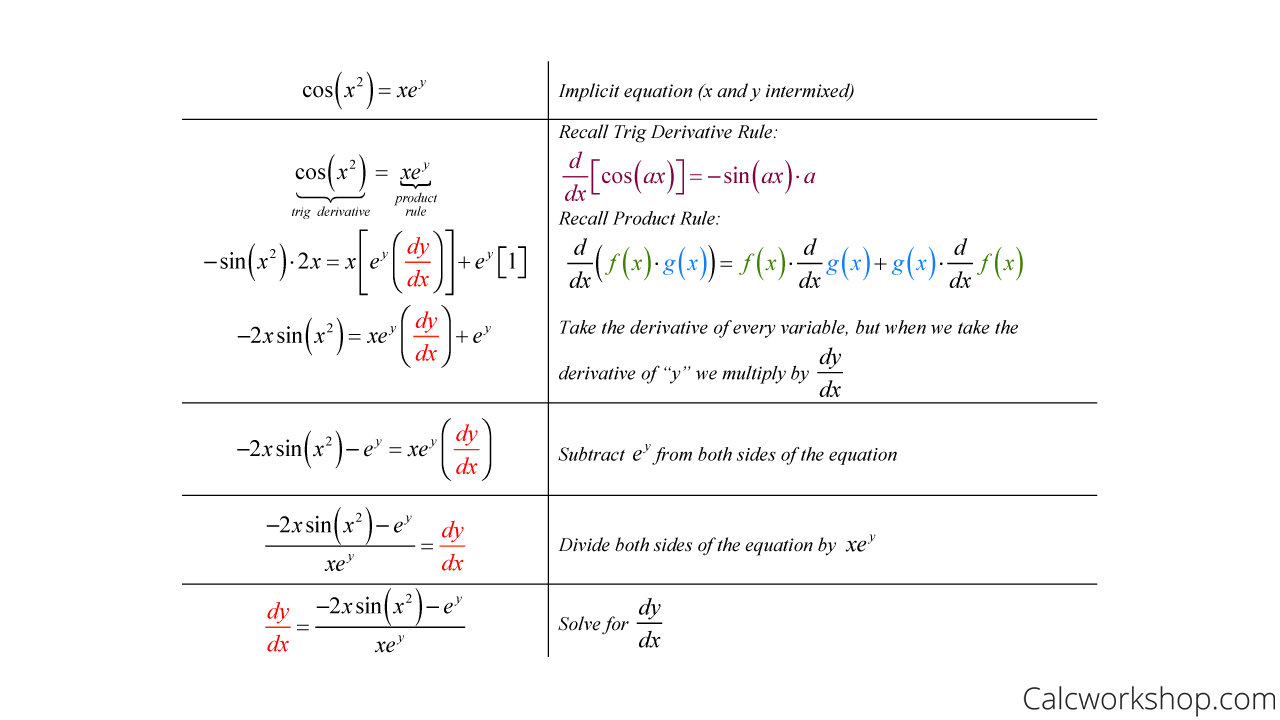Implicit Differentiation Of Partial Derivatives - So, if you can do calculus i derivatives you shouldn’t have too much. Partially differentiating both sides with respect to x: Perform implicit differentiation of a function of two or more variables. There are some situations when we have an equation implicitly defining a surface (meaning. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Z are related implicitly if they depend on each other by an equation of the. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Now let's try implicit differentiation: Fortunately, the concept of implicit differentiation for derivatives of single variable functions can.
There are some situations when we have an equation implicitly defining a surface (meaning. Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Now let's try implicit differentiation: So, if you can do calculus i derivatives you shouldn’t have too much. Z are related implicitly if they depend on each other by an equation of the. Partially differentiating both sides with respect to x: Perform implicit differentiation of a function of two or more variables.
Z are related implicitly if they depend on each other by an equation of the. Perform implicit differentiation of a function of two or more variables. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. So, if you can do calculus i derivatives you shouldn’t have too much. Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. Partially differentiating both sides with respect to x: $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. There are some situations when we have an equation implicitly defining a surface (meaning. Now let's try implicit differentiation:
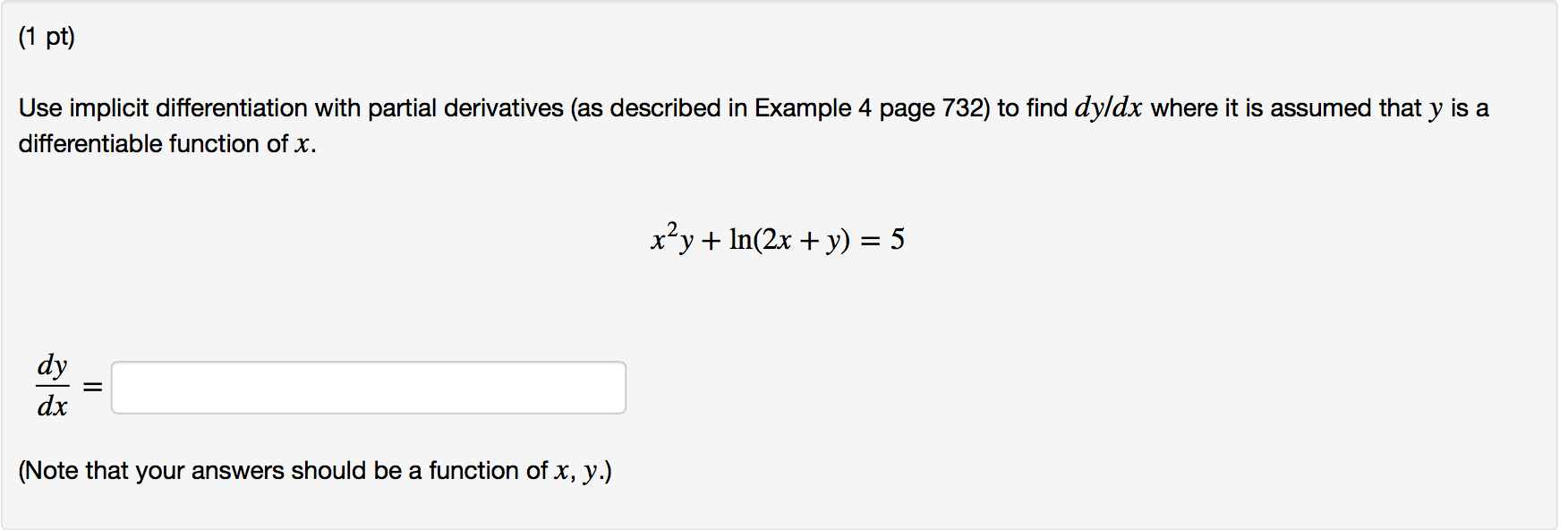
multivariable calculus Implicit differentiation with partial
$$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Z are related implicitly if they depend on each other by an equation of the. Partially differentiating both sides with respect to x: Perform implicit differentiation of a function of two or more variables. Now let's try implicit differentiation:
SOLUTION partial differentiation , partial derivatives , implicit
There are some situations when we have an equation implicitly defining a surface (meaning. Perform implicit differentiation of a function of two or more variables. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Now let's try implicit differentiation: Fortunately, the concept of implicit differentiation for derivatives of single variable functions can.
Solved Use implicit differentiation with partial derivatives
So, if you can do calculus i derivatives you shouldn’t have too much. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Now let's try implicit differentiation: Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. Z are related implicitly if they depend on each other by an equation of the.
Implicit Differentiation (w/ Examples And Worksheets!)
Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Perform implicit differentiation of a function of two or more variables. Partially differentiating both sides with respect to x:
calculus Implicit Partial Differentiation Mathematics Stack Exchange
Partially differentiating both sides with respect to x: Perform implicit differentiation of a function of two or more variables. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Z are related implicitly if they depend on each other by an equation of the. There are some situations when we have an equation implicitly defining a surface (meaning.
SOLUTION partial differentiation , partial derivatives , implicit
Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Z are related implicitly if they depend on each other by an equation of the. Now let's try implicit differentiation: Partially differentiating both sides with respect to x:
Explore IMPLICIT Differentiation & Function Theorem Calculus 3
There are some situations when we have an equation implicitly defining a surface (meaning. Z are related implicitly if they depend on each other by an equation of the. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Perform implicit differentiation of a function of two or more variables. $$ $$ 2x.
Partial Derivatives and Implicit differentiation 1
Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. So, if you can do calculus i derivatives you shouldn’t have too much. Now let's try implicit differentiation: There are some situations when we have an equation implicitly defining a.
SOLUTION partial differentiation , partial derivatives , implicit
Partially differentiating both sides with respect to x: Z are related implicitly if they depend on each other by an equation of the. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. So, if you can do calculus i derivatives you shouldn’t have too.
Implicit Differentiation (w/ Examples And Worksheets!)
$$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. There are some situations when we have an equation implicitly defining a surface (meaning. Now let's try implicit differentiation: Z are related implicitly if they depend on each other by an equation of the. So, if you can do calculus i derivatives you shouldn’t have too much.
So, If You Can Do Calculus I Derivatives You Shouldn’t Have Too Much.
There are some situations when we have an equation implicitly defining a surface (meaning. Z are related implicitly if they depend on each other by an equation of the. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Fortunately, the concept of implicit differentiation for derivatives of single variable functions can.
Perform Implicit Differentiation Of A Function Of Two Or More Variables.
Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Partially differentiating both sides with respect to x: Now let's try implicit differentiation: