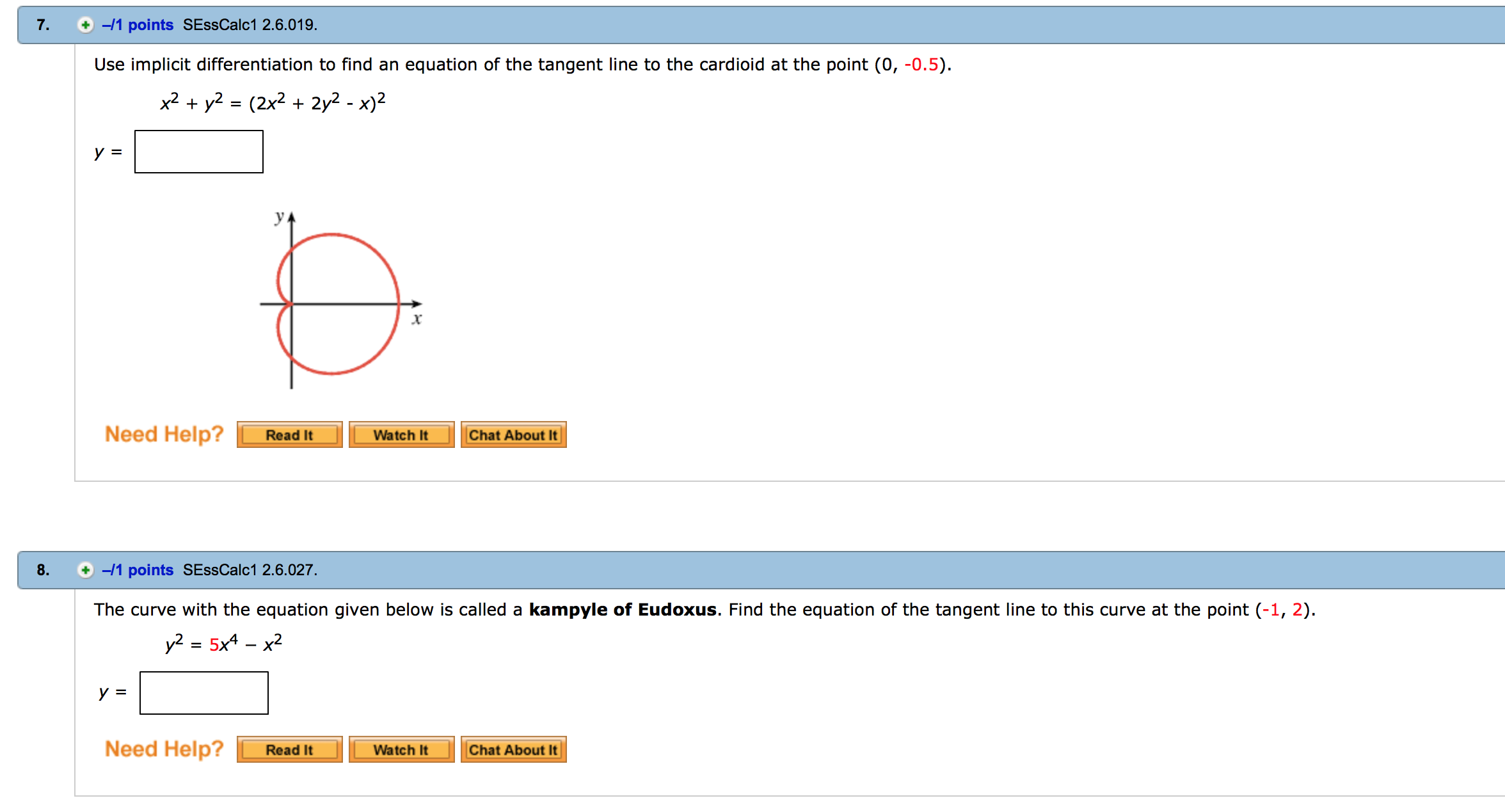
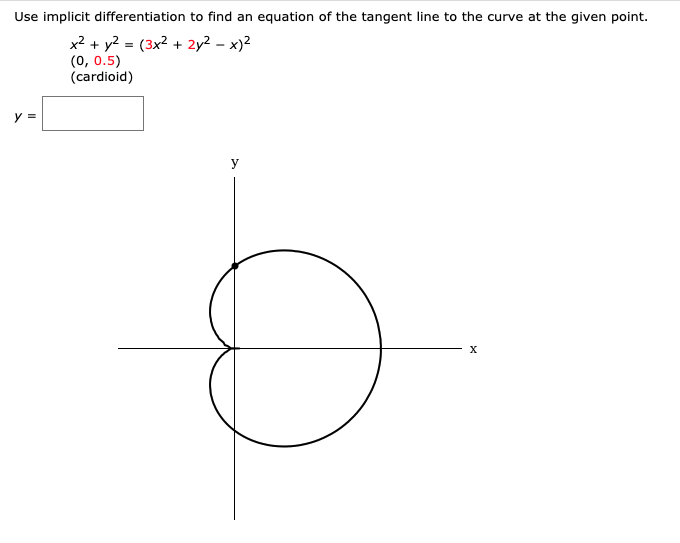
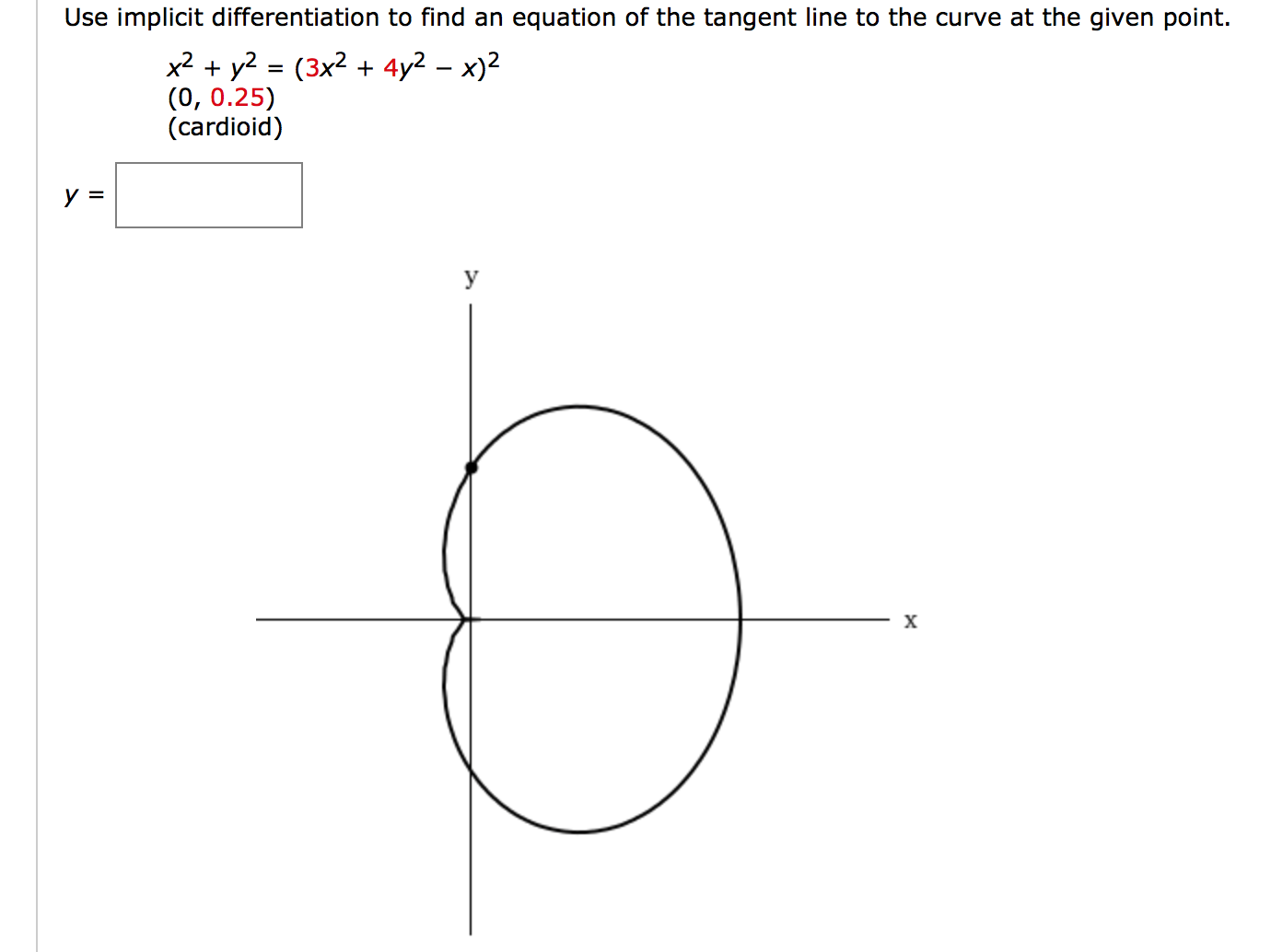
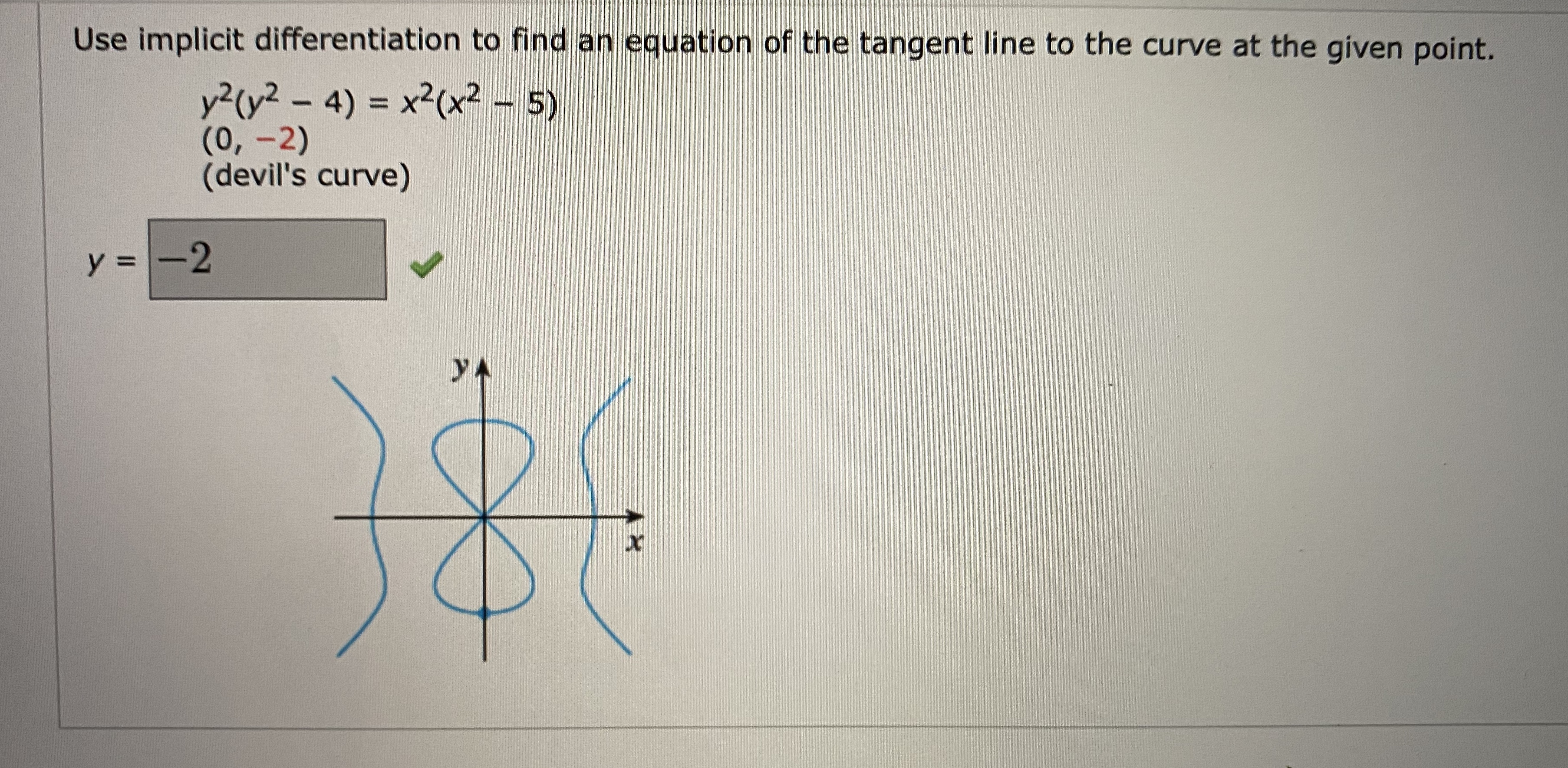
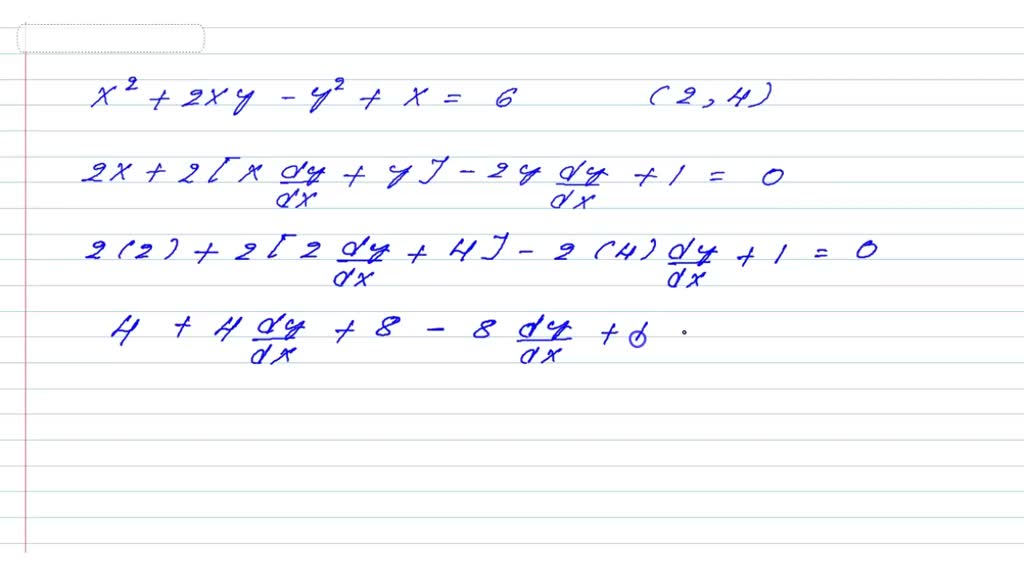How To Find Vertical Tangent Line Implicit Differentiation - Finding the vertical and horizontal tangent lines to an implicitly defined curve. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ The graph of z1 shown in lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a. Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x. The typical way to get used to implicit. In this article, we’ll show you how to find vertical and horizontal tangent lines using implicit differentiation. We find the first derivative and then consider the.
The graph of z1 shown in lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a. Finding the vertical and horizontal tangent lines to an implicitly defined curve. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ We find the first derivative and then consider the. In this article, we’ll show you how to find vertical and horizontal tangent lines using implicit differentiation. The typical way to get used to implicit. Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x.
Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ We find the first derivative and then consider the. Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x. Finding the vertical and horizontal tangent lines to an implicitly defined curve. In this article, we’ll show you how to find vertical and horizontal tangent lines using implicit differentiation. The graph of z1 shown in lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a. The typical way to get used to implicit.
Solved Use implicit differentiation to find an equation of
Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x. We find the first derivative and then consider the. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ The.
Solved Use Implicit Differentiation To Find An Equation O...
The graph of z1 shown in lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a. We find the first derivative and then consider the. Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x).
Answered Use implicit differentiation to find an… bartleby
Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x. The typical way to get used to implicit. The graph.
SOLVED Use implicit differentiation to find an equation of the tangent
The graph of z1 shown in lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a. In this article, we’ll show you how to find vertical and horizontal tangent lines using implicit differentiation. Finding the vertical and horizontal tangent lines to an implicitly defined curve. The typical way to.
Solved Use implicit differentiation to find an equation of
In this article, we’ll show you how to find vertical and horizontal tangent lines using implicit differentiation. We find the first derivative and then consider the. Finding the vertical and horizontal tangent lines to an implicitly defined curve. The typical way to get used to implicit. Ef (x) f ′ (x) = 1 and we can now solve for f.
Answered Use implicit differentiation to find an… bartleby
We find the first derivative and then consider the. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x. The.
Solved Use implicit differentiation to find an equation of
In this article, we’ll show you how to find vertical and horizontal tangent lines using implicit differentiation. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x).
Solved Use implicit differentiation to find an equation of
Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x. The graph of z1 shown in lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a. We find.
Answered Use implicit differentiation to find an… bartleby
Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x. The graph of z1 shown in lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a. We find.
SOLVED point) Use implicit differentiation to find an equation of the
We find the first derivative and then consider the. Ef (x) f ′ (x) = 1 and we can now solve for f ′ (x) f ′ (x) = e − f (x) = e − logx = 1 x. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ In.
Ef (X) F ′ (X) = 1 And We Can Now Solve For F ′ (X) F ′ (X) = E − F (X) = E − Logx = 1 X.
The graph of z1 shown in lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a. The typical way to get used to implicit. Finding the vertical and horizontal tangent lines to an implicitly defined curve. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$
We Find The First Derivative And Then Consider The.
In this article, we’ll show you how to find vertical and horizontal tangent lines using implicit differentiation.