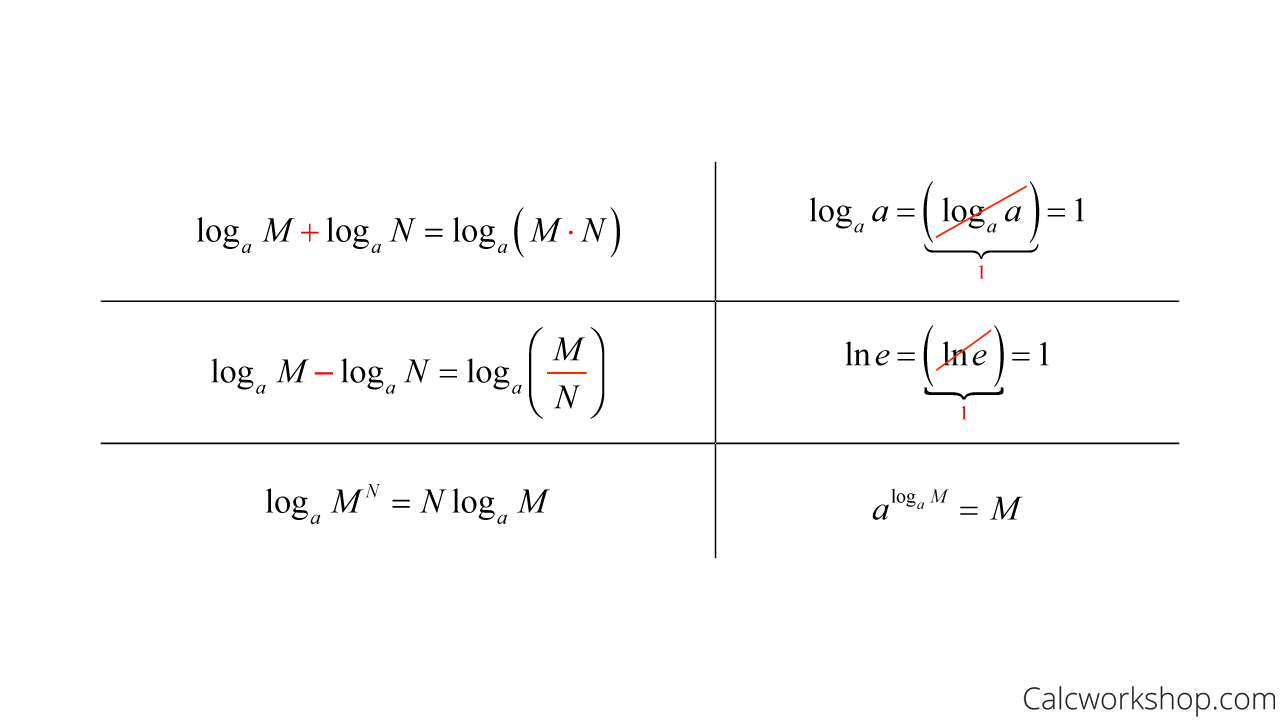
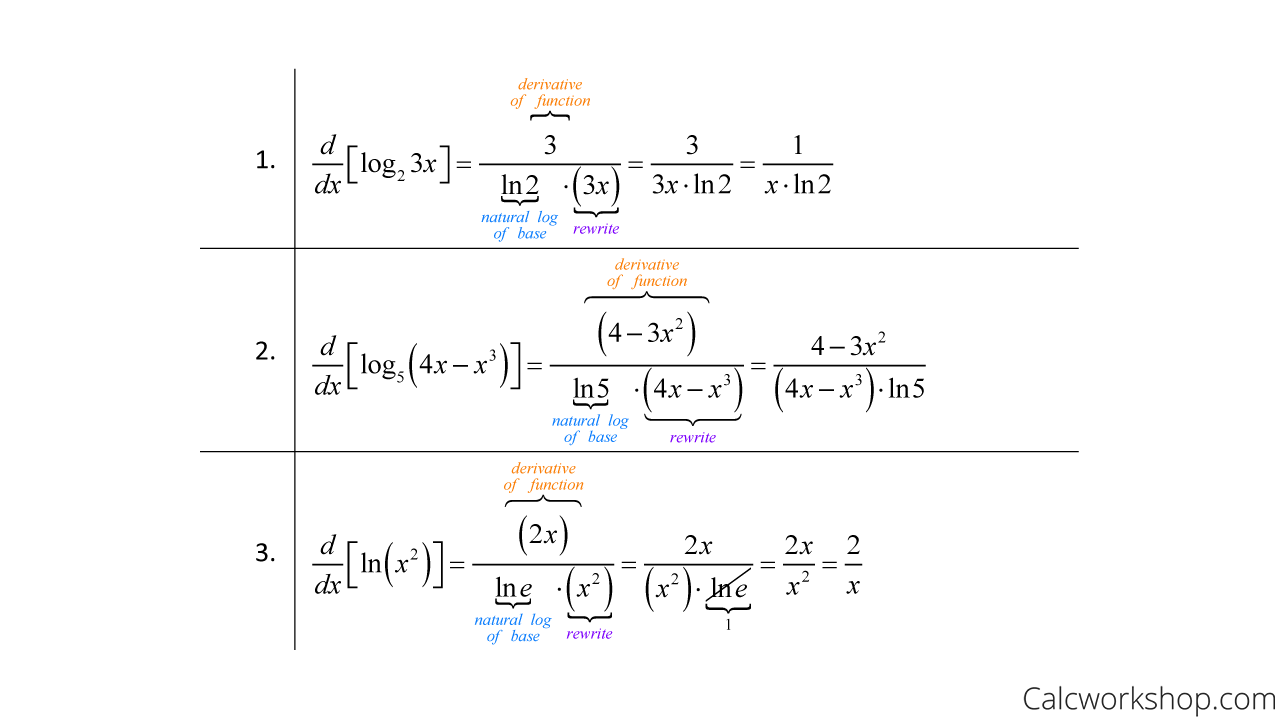
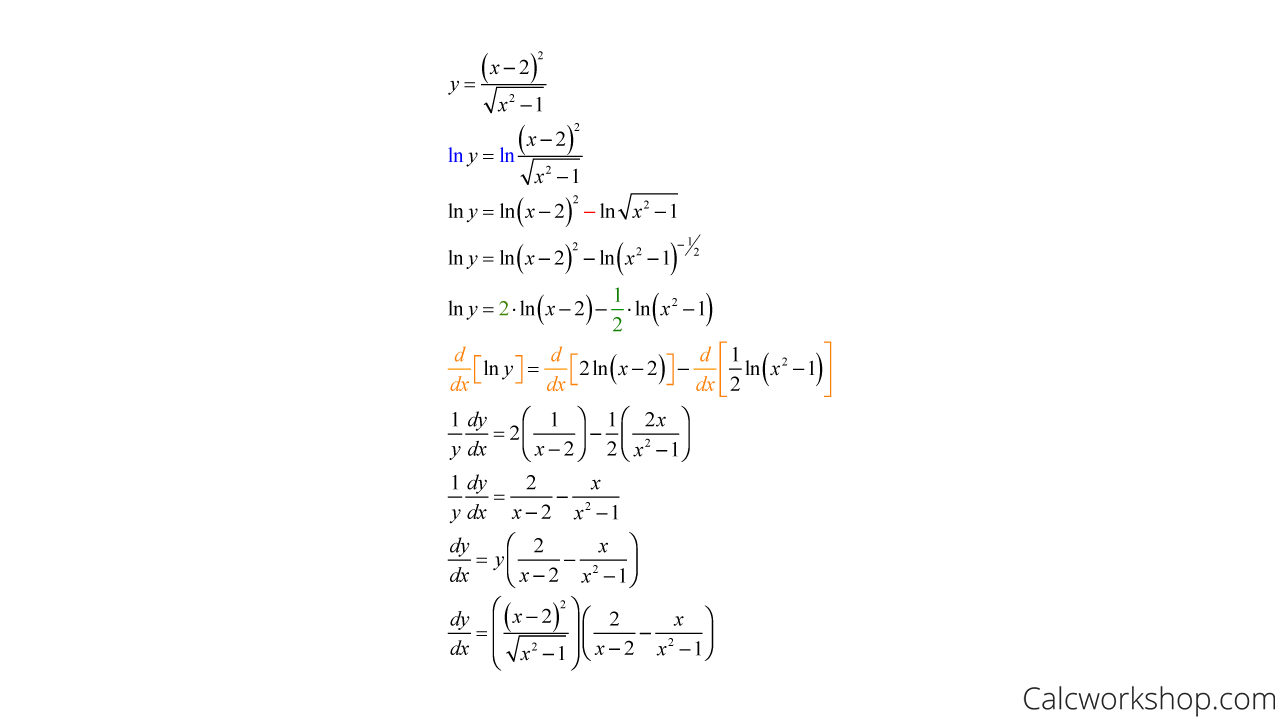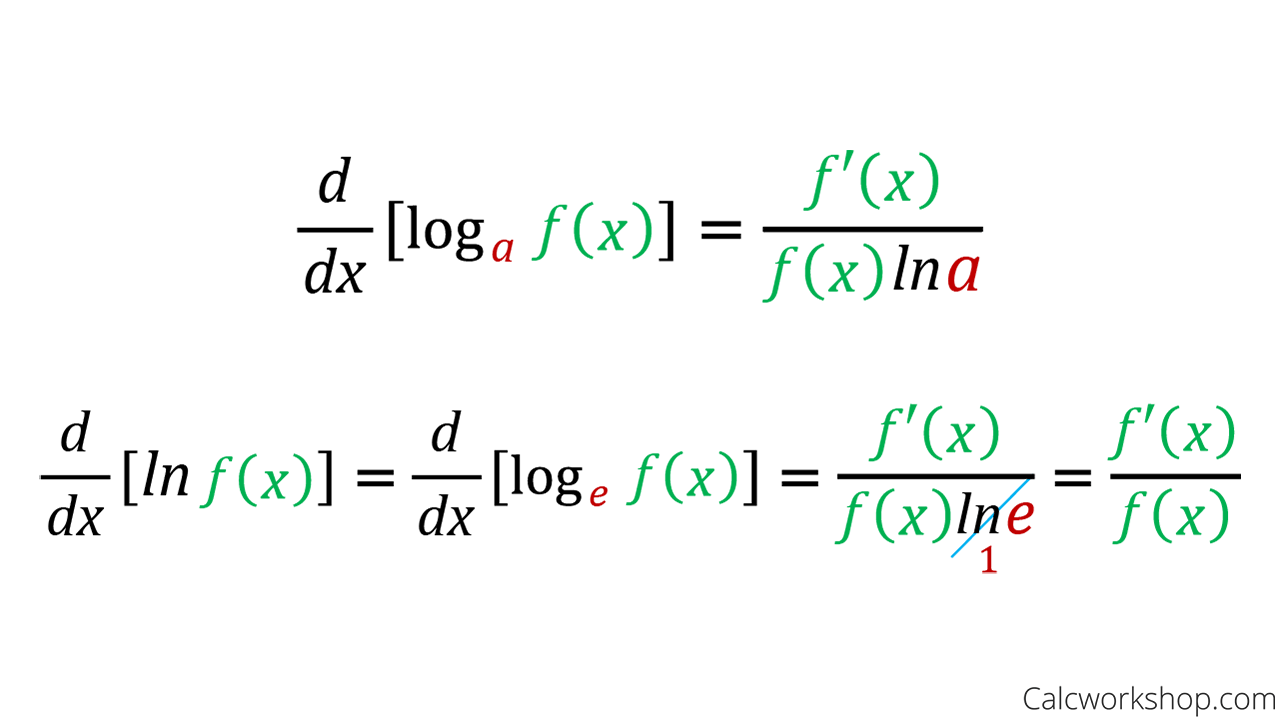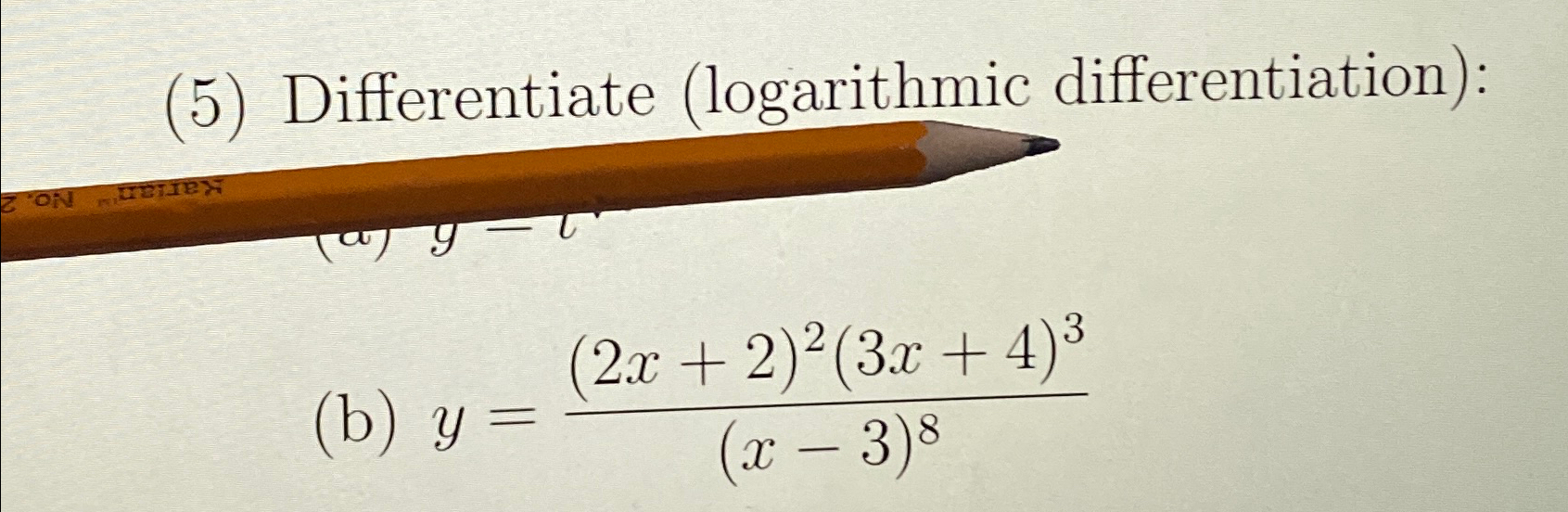How To Differentiate Logarithmic Functions - Find $$f'(x)$$ by first expanding the function and then differentiating. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of.
Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Find $$f'(x)$$ by first expanding the function and then differentiating. We can also use logarithmic differentiation to differentiate functions in the form. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of.
Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. We can also use logarithmic differentiation to differentiate functions in the form. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Find $$f'(x)$$ by first expanding the function and then differentiating.
Differentiation of Logarithmic Functions AlvinexReed
\[y = {\left( {f\left( x \right)} \right)^{g\left(. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Find $$f'(x)$$ by first expanding the function and then differentiating.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Find $$f'(x)$$ by first expanding the function and then differentiating.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Find $$f'(x)$$ by first expanding the function and then differentiating. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by.
PPT Calculus Section 5.4 Differentiate logarithmic functions
Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. We can also use logarithmic differentiation to differentiate functions in the form. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. \[y = {\left( {f\left( x.
Derivatives of Logarithmic Functions (Fully Explained!)
\[y = {\left( {f\left( x \right)} \right)^{g\left(. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. We can also use logarithmic differentiation to differentiate functions in.
Derivatives of Logarithmic Functions (Fully Explained!)
Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Find $$f'(x)$$ by first expanding the function and then differentiating. \[y = {\left( {f\left( x \right)} \right)^{g\left(.
Derivatives of Logarithmic Functions
We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2.
Solved (5) Differentiate (logarithmic
Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Find $$f'(x)$$ by first expanding the function and then differentiating. \[y = {\left( {f\left( x \right)} \right)^{g\left(. We can also use logarithmic differentiation to differentiate functions in the form.
Derivatives of Logarithmic Functions (Fully Explained!)
Find $$f'(x)$$ by first expanding the function and then differentiating. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. We can also use logarithmic differentiation to differentiate functions in the form. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Find $$f'(x)$$ by first expanding the function and then differentiating. \[y = {\left(.
\[Y = {\Left( {F\Left( X \Right)} \Right)^{G\Left(.
Find $$f'(x)$$ by first expanding the function and then differentiating. We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$.