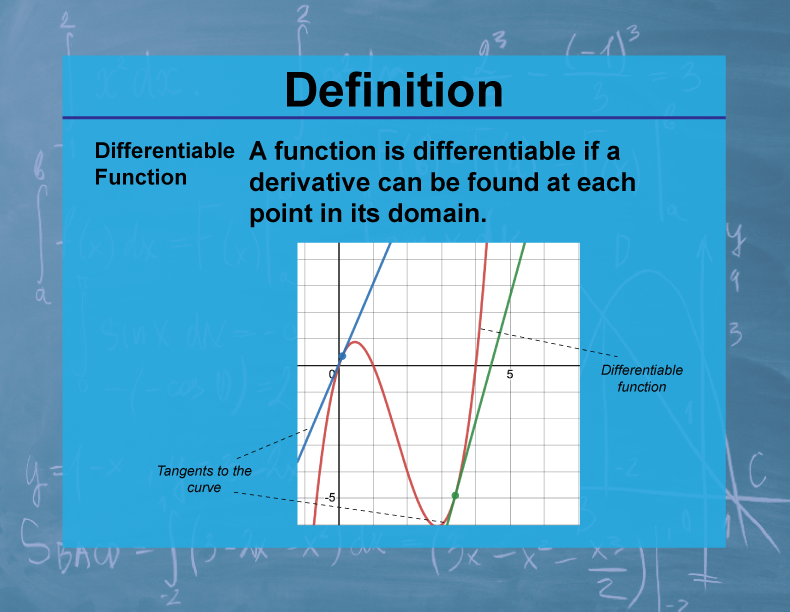
How Is A Function Differentiable - Simply put, differentiable means the derivative exists at every point in its domain. Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. As question given f(x) = [x] where x is greater than. A function is differentiable if the derivative exists at all points for which it is defined, but what does this actually mean? In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. So the function g(x) = |x| with domain (0, +∞) is differentiable. Consequently, the only way for the derivative to exist is if the function also exists (i.e., is.
A function is differentiable if the derivative exists at all points for which it is defined, but what does this actually mean? So the function g(x) = |x| with domain (0, +∞) is differentiable. As question given f(x) = [x] where x is greater than. Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. Consequently, the only way for the derivative to exist is if the function also exists (i.e., is. Simply put, differentiable means the derivative exists at every point in its domain.
Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. Simply put, differentiable means the derivative exists at every point in its domain. So the function g(x) = |x| with domain (0, +∞) is differentiable. As question given f(x) = [x] where x is greater than. In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. A function is differentiable if the derivative exists at all points for which it is defined, but what does this actually mean? Consequently, the only way for the derivative to exist is if the function also exists (i.e., is.
DefinitionCalculus TopicsDifferentiable Function Media4Math
So the function g(x) = |x| with domain (0, +∞) is differentiable. As question given f(x) = [x] where x is greater than. Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. A function is differentiable if the derivative exists at.
Differentiable vs. Continuous Functions Understanding the Distinctions
Simply put, differentiable means the derivative exists at every point in its domain. Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. As question given f(x) = [x] where x is greater than. So the function g(x) = |x| with domain.
A function differentiable along every line through
Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. Consequently, the only way for the derivative to exist is if.
Differentiable Function Meaning, Formulas and Examples Outlier
So the function g(x) = |x| with domain (0, +∞) is differentiable. Consequently, the only way for the derivative to exist is if the function also exists (i.e., is. As question given f(x) = [x] where x is greater than. Simply put, differentiable means the derivative exists at every point in its domain. Prove that the greatest integer function defined.
Differentiable Function CBSE Library
A function is differentiable if the derivative exists at all points for which it is defined, but what does this actually mean? Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. Simply put, differentiable means the derivative exists at every point.
Differentiable function Wikiwand
Simply put, differentiable means the derivative exists at every point in its domain. A function is differentiable if the derivative exists at all points for which it is defined, but what does this actually mean? In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. As question given f(x).
Differentiable Function Meaning, Formulas and Examples Outlier
As question given f(x) = [x] where x is greater than. Simply put, differentiable means the derivative exists at every point in its domain. So the function g(x) = |x| with domain (0, +∞) is differentiable. Consequently, the only way for the derivative to exist is if the function also exists (i.e., is. A function is differentiable if the derivative.
Twice Continuously Differentiable Function
As question given f(x) = [x] where x is greater than. Consequently, the only way for the derivative to exist is if the function also exists (i.e., is. In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. So the function g(x) = |x| with domain (0, +∞) is.
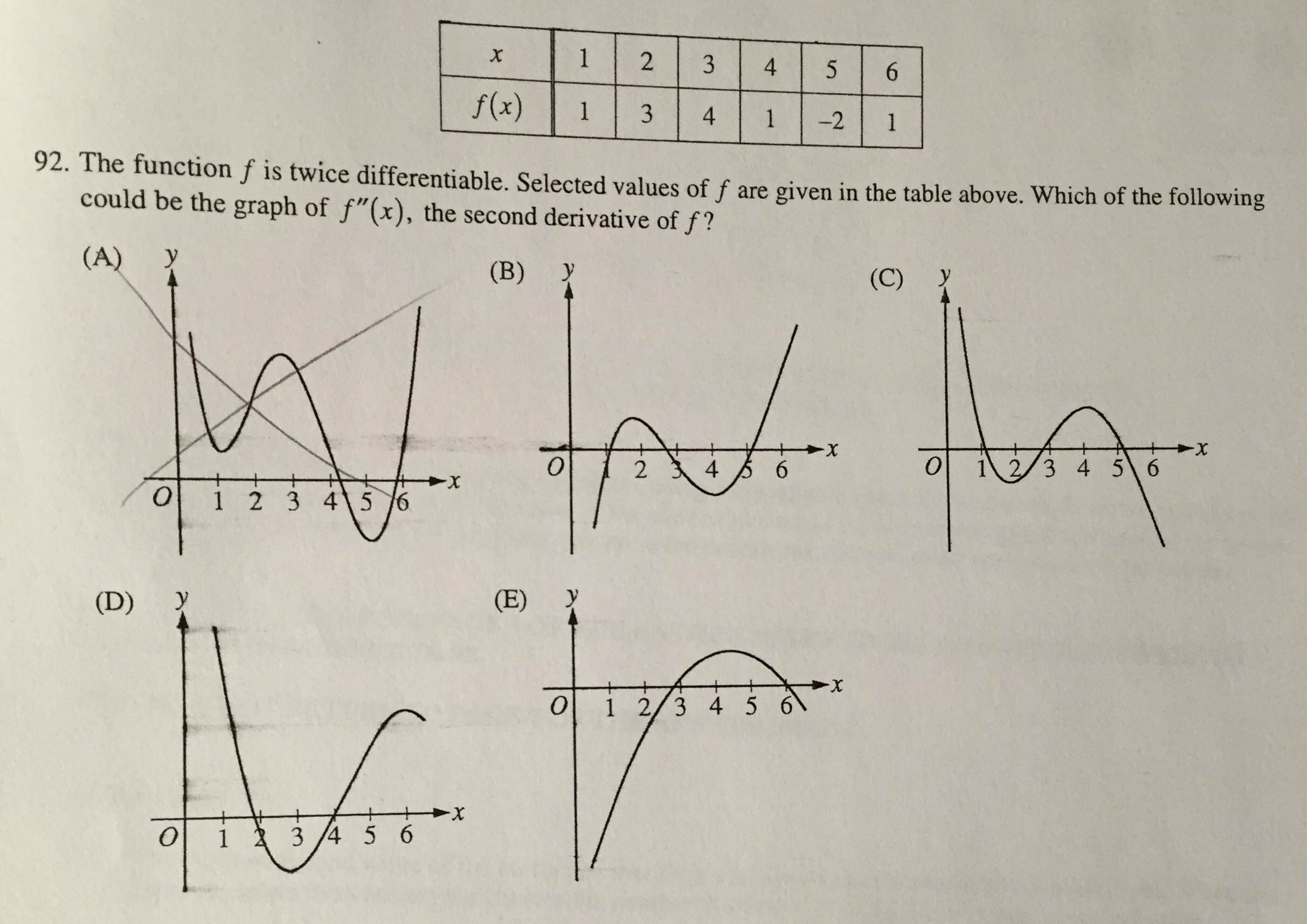
Solved Let f(x) be a differentiable function possessing an
Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. So the function g(x) = |x| with domain (0, +∞) is differentiable. In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its.
Differentiable Function A Plus Topper
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. Consequently, the only way for the derivative to exist is if the function also exists (i.e., is. A function is differentiable if the derivative exists at all points for which it is defined, but what does this actually mean?.
Simply Put, Differentiable Means The Derivative Exists At Every Point In Its Domain.
As question given f(x) = [x] where x is greater than. A function is differentiable if the derivative exists at all points for which it is defined, but what does this actually mean? Prove that the greatest integer function defined by f(x) = [x] , 0 < x < 3 is not differentiable at x = 1 and x = 2. In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain.
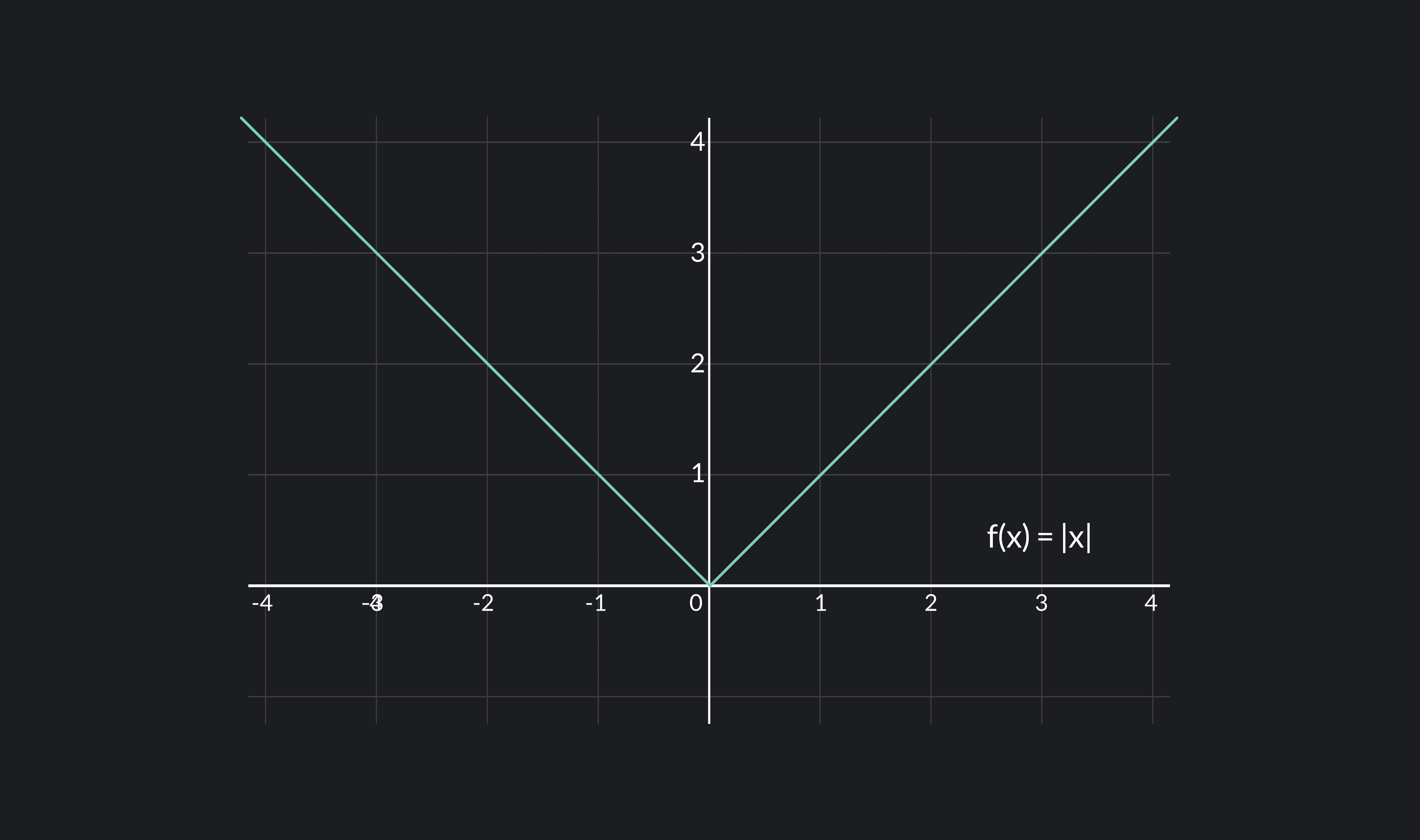
So The Function G(X) = |X| With Domain (0, +∞) Is Differentiable.
Consequently, the only way for the derivative to exist is if the function also exists (i.e., is.