Homogeneous Vs Nonhomogeneous Differential Equation

Homogeneous Vs Nonhomogeneous Differential Equation - The terminology and methods are different from. The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: This is another way of classifying differential equations. That is, if no term is a. In this section, we examine how to solve nonhomogeneous differential equations. A linear equation may further be called homogeneous if all terms depend on the dependent variable. If \( f(x) = 0 \), then it is called a homogeneous equation.

This is another way of classifying differential equations. A linear equation may further be called homogeneous if all terms depend on the dependent variable. The terminology and methods are different from. In this section, we examine how to solve nonhomogeneous differential equations. That is, if no term is a. The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: If \( f(x) = 0 \), then it is called a homogeneous equation.

The terminology and methods are different from. A linear equation may further be called homogeneous if all terms depend on the dependent variable. That is, if no term is a. The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: If \( f(x) = 0 \), then it is called a homogeneous equation. This is another way of classifying differential equations. In this section, we examine how to solve nonhomogeneous differential equations.

[Solved] A nonhomogeneous differential equation, a complementary

In this section, we examine how to solve nonhomogeneous differential equations. This is another way of classifying differential equations. The terminology and methods are different from. The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: If \( f(x) = 0 \), then it is called a homogeneous equation.

Solved In Problems 21 through 24, a nonhomogeneous

The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: This is another way of classifying differential equations. A linear equation may further be called homogeneous if all terms depend on the dependent variable. That is, if no term is a. In this section, we examine how to solve nonhomogeneous differential.

[Solved] Find the general solution to the nonhomogeneous differential

This is another way of classifying differential equations. The terminology and methods are different from. If \( f(x) = 0 \), then it is called a homogeneous equation. A linear equation may further be called homogeneous if all terms depend on the dependent variable. That is, if no term is a.

[Differential Equations] NonHomogeneous Equation Solution r/learnmath

If \( f(x) = 0 \), then it is called a homogeneous equation. The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: That is, if no term is a. This is another way of classifying differential equations. In this section, we examine how to solve nonhomogeneous differential equations.

Solving a nonhomogeneous equation

A linear equation may further be called homogeneous if all terms depend on the dependent variable. That is, if no term is a. In this section, we examine how to solve nonhomogeneous differential equations. If \( f(x) = 0 \), then it is called a homogeneous equation. This is another way of classifying differential equations.

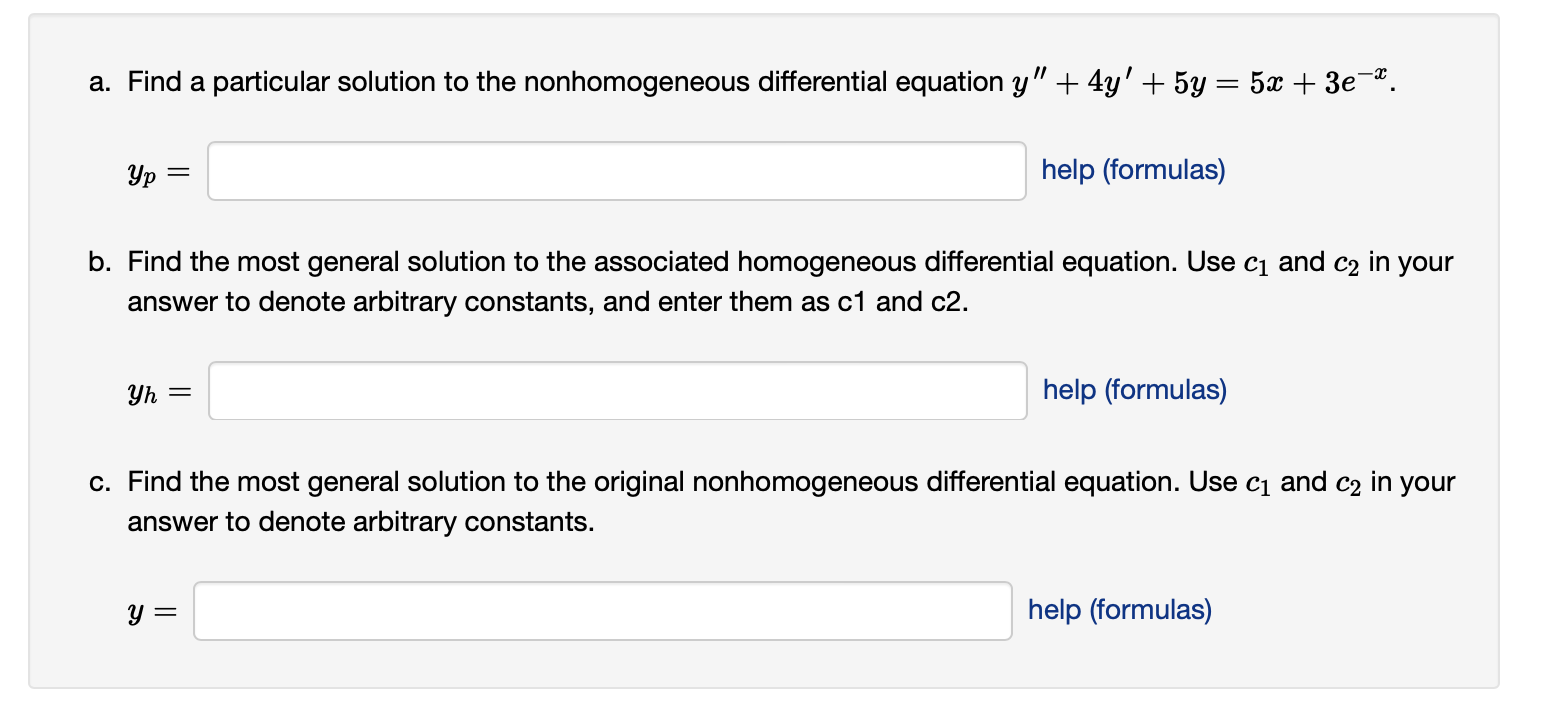
Solved a. Find a particular solution to the nonhomogeneous

If \( f(x) = 0 \), then it is called a homogeneous equation. The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: That is, if no term is a. The terminology and methods are different from. A linear equation may further be called homogeneous if all terms depend on the.

Particular Solution of NonHomogeneous Differential Equations Mr

This is another way of classifying differential equations. In this section, we examine how to solve nonhomogeneous differential equations. A linear equation may further be called homogeneous if all terms depend on the dependent variable. That is, if no term is a. If \( f(x) = 0 \), then it is called a homogeneous equation.

The homogeneous differential equation (Equation (16)) has non trivial

If \( f(x) = 0 \), then it is called a homogeneous equation. The terminology and methods are different from. In this section, we examine how to solve nonhomogeneous differential equations. This is another way of classifying differential equations. A linear equation may further be called homogeneous if all terms depend on the dependent variable.

PPT Homogeneous Differential Equation NonHomogeneous Differential

That is, if no term is a. The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: If \( f(x) = 0 \), then it is called a homogeneous equation. A linear equation may further be called homogeneous if all terms depend on the dependent variable. This is another way of.

Differential Equations Lecture NonHomogeneous Linear Differential E…

A linear equation may further be called homogeneous if all terms depend on the dependent variable. In this section, we examine how to solve nonhomogeneous differential equations. The simplest test of homogeneity, and definition at the same time, not only for differential equations, is the following: That is, if no term is a. The terminology and methods are different from.

The Terminology And Methods Are Different From.

In this section, we examine how to solve nonhomogeneous differential equations. This is another way of classifying differential equations. That is, if no term is a. If \( f(x) = 0 \), then it is called a homogeneous equation.