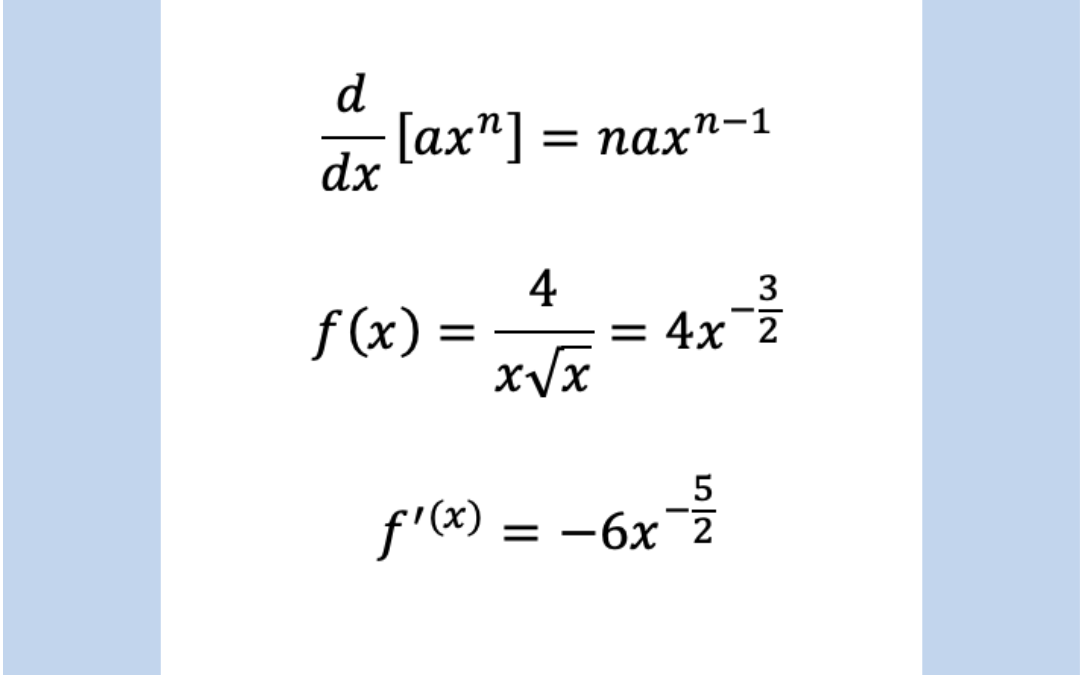Hard Differentiation Problems - In the following problems you will find it helpful to make an equation of the form y = ::: F(x) = 1 x5 −3x+2. And take a natural logarithm of both sides before. F(x) = 5−3x+2x3 x2 +4 53. F(x) = x+1 x−1 54. Here is a set of practice problems to accompany the higher order derivatives section of the derivatives chapter of the notes. F(x) = x3 x3 +2 55. You can write the derivative of p xeither as. Madas question 3 differentiate the following expressions with respect to x a) y x x= −2 64 2 24 5 dy x x. F(x) = 3x−2 x3 +3x 52.
Here is a set of practice problems to accompany the higher order derivatives section of the derivatives chapter of the notes. F(x) = 5−3x+2x3 x2 +4 53. F(x) = x+1 x−1 54. Practising these questions will help students to solve hard problems and to score more marks in the exam. The differentiation of a function f (x). We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation. You can write the derivative of p xeither as. F(x) = 3x−2 x3 +3x 52. F(x) = 1 x5 −3x+2. In the following problems you will find it helpful to make an equation of the form y = :::
We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation. F(x) = 5−3x+2x3 x2 +4 53. Practising these questions will help students to solve hard problems and to score more marks in the exam. And take a natural logarithm of both sides before. In the following problems you will find it helpful to make an equation of the form y = ::: F(x) = 1 x5 −3x+2. F(x) = x3 x3 +2 55. F(x) = 3x−2 x3 +3x 52. F(x) = x+1 x−1 54. The differentiation of a function f (x).
Differentiation Rules
In the following problems you will find it helpful to make an equation of the form y = ::: You can write the derivative of p xeither as. And take a natural logarithm of both sides before. The differentiation of a function f (x). F(x) = x+1 x−1 54.
How to solve Differentiation problems easily (Part 01)
And take a natural logarithm of both sides before. The differentiation of a function f (x). We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation. F(x) = 1 x5 −3x+2. F(x) = 5−3x+2x3 x2 +4 53.
Implicit Differentiation Formula Examples
F(x) = x3 x3 +2 55. F(x) = 3x−2 x3 +3x 52. Here is a set of practice problems to accompany the higher order derivatives section of the derivatives chapter of the notes. F(x) = x+1 x−1 54. Madas question 3 differentiate the following expressions with respect to x a) y x x= −2 64 2 24 5 dy x.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
In the following problems you will find it helpful to make an equation of the form y = ::: F(x) = 1 x5 −3x+2. F(x) = x3 x3 +2 55. Here is a set of practice problems to accompany the higher order derivatives section of the derivatives chapter of the notes. The differentiation of a function f (x).
Implicit Differentiation Problems And Answers
We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation. F(x) = 3x−2 x3 +3x 52. Here is a set of practice problems to accompany the higher order derivatives section of the derivatives chapter of the notes. You can write the derivative of p xeither as. F(x) = 1 x5 −3x+2.
How to Do Implicit Differentiation 7 Steps (with Pictures)
F(x) = x+1 x−1 54. Practising these questions will help students to solve hard problems and to score more marks in the exam. F(x) = x3 x3 +2 55. We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation. F(x) = 3x−2 x3 +3x 52.
Differentiation
F(x) = x+1 x−1 54. We also cover implicit differentiation, related rates, higher order derivatives and logarithmic differentiation. F(x) = 5−3x+2x3 x2 +4 53. In the following problems you will find it helpful to make an equation of the form y = ::: And take a natural logarithm of both sides before.
Parametric Differentiation Questions Revisely
The differentiation of a function f (x). F(x) = 5−3x+2x3 x2 +4 53. F(x) = x3 x3 +2 55. In the following problems you will find it helpful to make an equation of the form y = ::: F(x) = 3x−2 x3 +3x 52.
Differentiation Is Hard But Necessary. (Don’t Worry, There’s Help
F(x) = 5−3x+2x3 x2 +4 53. Practising these questions will help students to solve hard problems and to score more marks in the exam. You can write the derivative of p xeither as. F(x) = 1 x5 −3x+2. F(x) = x3 x3 +2 55.
Differentiation Questions and Answers My Maths Guy
Practising these questions will help students to solve hard problems and to score more marks in the exam. The differentiation of a function f (x). F(x) = 1 x5 −3x+2. F(x) = 3x−2 x3 +3x 52. F(x) = x+1 x−1 54.
And Take A Natural Logarithm Of Both Sides Before.
Here is a set of practice problems to accompany the higher order derivatives section of the derivatives chapter of the notes. Madas question 3 differentiate the following expressions with respect to x a) y x x= −2 64 2 24 5 dy x x. F(x) = x3 x3 +2 55. Practising these questions will help students to solve hard problems and to score more marks in the exam.
F(X) = 3X−2 X3 +3X 52.
F(x) = x+1 x−1 54. F(x) = 5−3x+2x3 x2 +4 53. You can write the derivative of p xeither as. F(x) = 1 x5 −3x+2.
We Also Cover Implicit Differentiation, Related Rates, Higher Order Derivatives And Logarithmic Differentiation.
The differentiation of a function f (x). In the following problems you will find it helpful to make an equation of the form y = :::