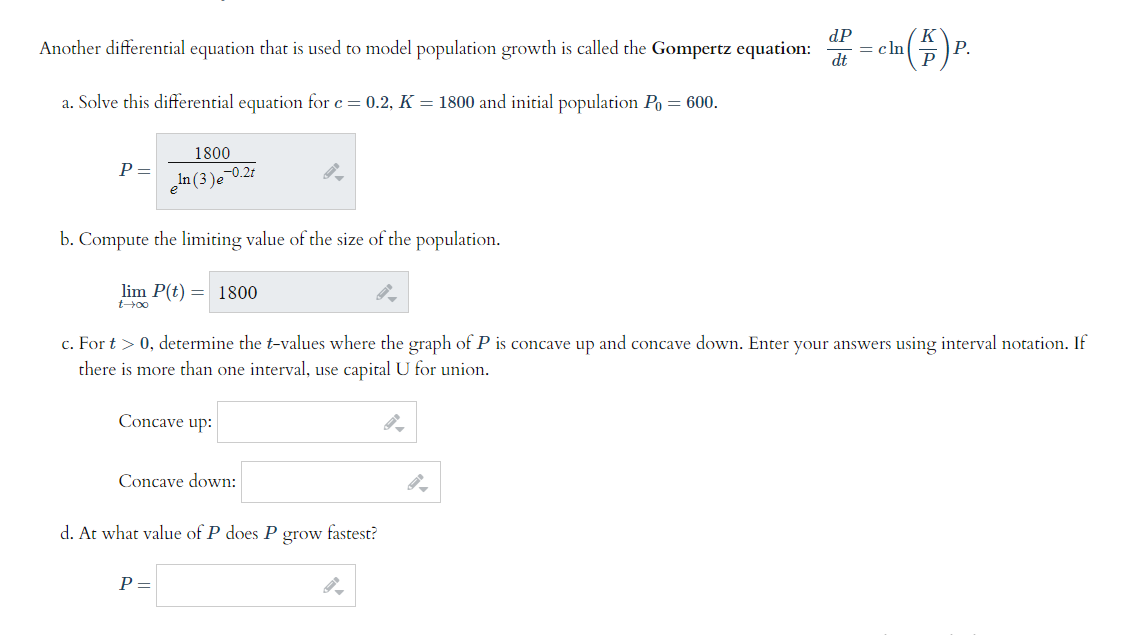
Gompertz Function Differential Equation - Stochastic models included are the gompertz, linear models with multiplicative noise term, the revised exponential and the generalized. $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. What is the general solution of this differential equation? \( x^{\prime}(t) = \alpha \log\left( \frac{k}{x(t)}. It is easy to verify that the dynamics of x(t) is governed by the gompertz differential equation: That is, i will allow the initial time to. The gompertz equation the evolution of the number of cells n in a growing tumor is often described by the gompertz equation a n ln(b n),. Dp(t) dt = p(t)(a − blnp(t)) with initial condition. Another model for a growth function for a limited population is given by the gompertz function, which is a solution to the differential equation. I'll solve the gomptertz equation.
I'll solve the gomptertz equation. The gompertz equation the evolution of the number of cells n in a growing tumor is often described by the gompertz equation a n ln(b n),. Stochastic models included are the gompertz, linear models with multiplicative noise term, the revised exponential and the generalized. Another model for a growth function for a limited population is given by the gompertz function, which is a solution to the differential equation. Dp(t) dt = p(t)(a − blnp(t)) with initial condition. $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. \( x^{\prime}(t) = \alpha \log\left( \frac{k}{x(t)}. That is, i will allow the initial time to. What is the general solution of this differential equation? It is easy to verify that the dynamics of x(t) is governed by the gompertz differential equation:
What is the general solution of this differential equation? Another model for a growth function for a limited population is given by the gompertz function, which is a solution to the differential equation. $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. That is, i will allow the initial time to. \( x^{\prime}(t) = \alpha \log\left( \frac{k}{x(t)}. Stochastic models included are the gompertz, linear models with multiplicative noise term, the revised exponential and the generalized. It is easy to verify that the dynamics of x(t) is governed by the gompertz differential equation: I'll solve the gomptertz equation. Dp(t) dt = p(t)(a − blnp(t)) with initial condition. The gompertz equation the evolution of the number of cells n in a growing tumor is often described by the gompertz equation a n ln(b n),.
The Gompertz differential equation, a model for restricted p Quizlet
$$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. It is easy to verify that the dynamics of x(t) is governed by the gompertz differential equation: Dp(t) dt = p(t)(a − blnp(t)) with initial condition. Stochastic models included are the gompertz, linear models with multiplicative noise term, the revised exponential and the generalized. \( x^{\prime}(t) = \alpha \log\left( \frac{k}{x(t)}.
Solved Another differential equation that is used to model
What is the general solution of this differential equation? Another model for a growth function for a limited population is given by the gompertz function, which is a solution to the differential equation. Dp(t) dt = p(t)(a − blnp(t)) with initial condition. $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. The gompertz equation the evolution of the number of.
Solved Another differential equation that is used to model
Dp(t) dt = p(t)(a − blnp(t)) with initial condition. It is easy to verify that the dynamics of x(t) is governed by the gompertz differential equation: I'll solve the gomptertz equation. $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. Another model for a growth function for a limited population is given by the gompertz function, which is a solution.
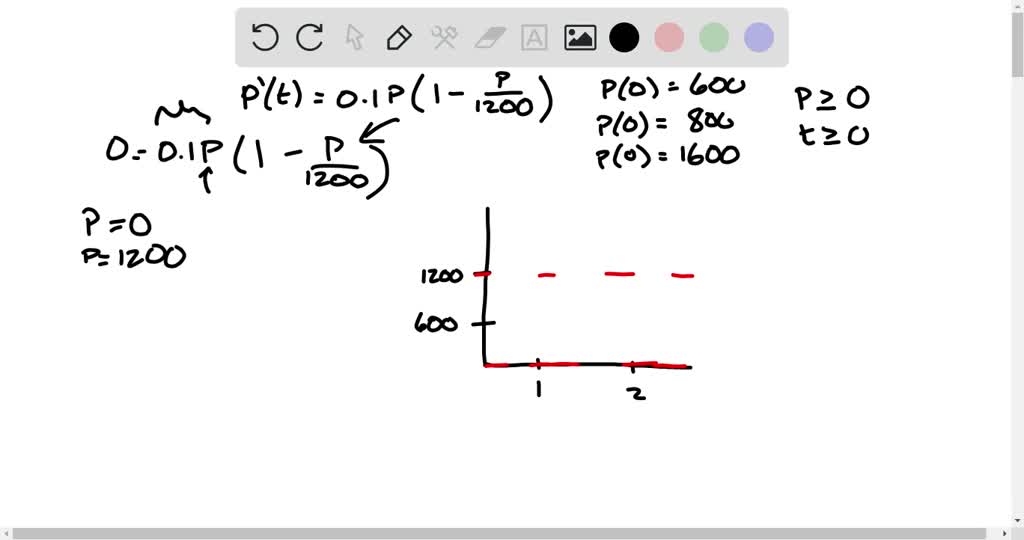
Solved (a) Suppose a=b=1 in the Gompertz differential
Dp(t) dt = p(t)(a − blnp(t)) with initial condition. Stochastic models included are the gompertz, linear models with multiplicative noise term, the revised exponential and the generalized. $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. That is, i will allow the initial time to. I'll solve the gomptertz equation.
Top 11 Gompertz Differential Equation Quotes & Sayings
Stochastic models included are the gompertz, linear models with multiplicative noise term, the revised exponential and the generalized. The gompertz equation the evolution of the number of cells n in a growing tumor is often described by the gompertz equation a n ln(b n),. What is the general solution of this differential equation? \( x^{\prime}(t) = \alpha \log\left( \frac{k}{x(t)}. That.
Solved Another differential equation that is used to model
I'll solve the gomptertz equation. \( x^{\prime}(t) = \alpha \log\left( \frac{k}{x(t)}. The gompertz equation the evolution of the number of cells n in a growing tumor is often described by the gompertz equation a n ln(b n),. Another model for a growth function for a limited population is given by the gompertz function, which is a solution to the differential.
[Solved] 9. Obtain the solution of the Gompertz growth mo
Another model for a growth function for a limited population is given by the gompertz function, which is a solution to the differential equation. $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. The gompertz equation the evolution of the number of cells n in a growing tumor is often described by the gompertz equation a n ln(b n),. It.
Solved dP Another differential equation that is used to
$$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. That is, i will allow the initial time to. Dp(t) dt = p(t)(a − blnp(t)) with initial condition. I'll solve the gomptertz equation. What is the general solution of this differential equation?
SOLVEDRefer to Exercise 18 . Consider the Gompertz differential
It is easy to verify that the dynamics of x(t) is governed by the gompertz differential equation: $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. What is the general solution of this differential equation? The gompertz equation the evolution of the number of cells n in a growing tumor is often described by the gompertz equation a n ln(b.
Incredible Gompertz Differential Equation References
Another model for a growth function for a limited population is given by the gompertz function, which is a solution to the differential equation. What is the general solution of this differential equation? $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. It is easy to verify that the dynamics of x(t) is governed by the gompertz differential equation: I'll.
It Is Easy To Verify That The Dynamics Of X(T) Is Governed By The Gompertz Differential Equation:
What is the general solution of this differential equation? $$ \frac{dy}{dt} = k \enspace y \enspace \ln(\frac{a}{y})$$ where. That is, i will allow the initial time to. I'll solve the gomptertz equation.
Dp(T) Dt = P(T)(A − Blnp(T)) With Initial Condition.
The gompertz equation the evolution of the number of cells n in a growing tumor is often described by the gompertz equation a n ln(b n),. Another model for a growth function for a limited population is given by the gompertz function, which is a solution to the differential equation. Stochastic models included are the gompertz, linear models with multiplicative noise term, the revised exponential and the generalized. \( x^{\prime}(t) = \alpha \log\left( \frac{k}{x(t)}.





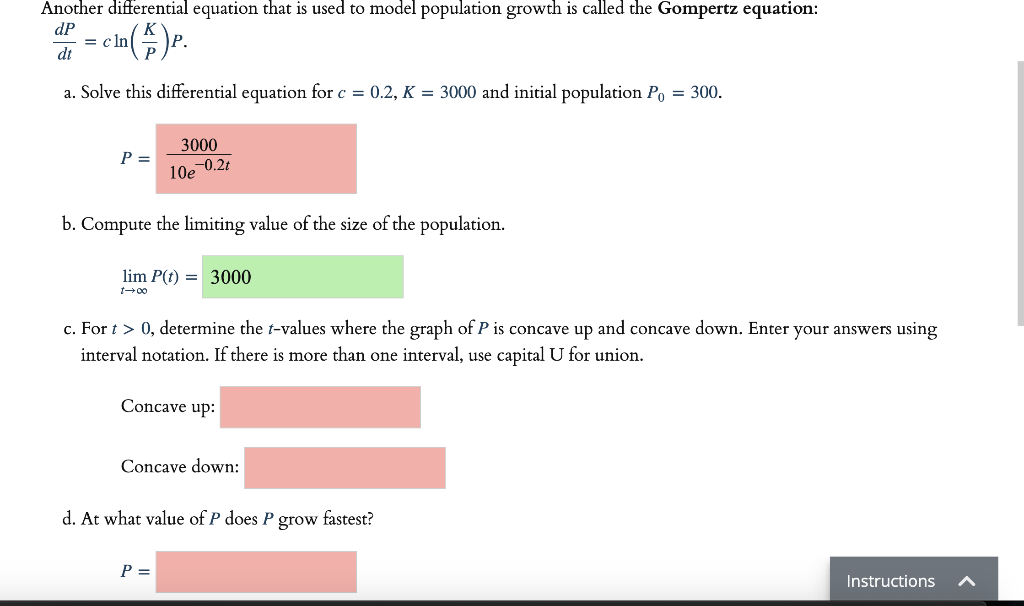
![[Solved] 9. Obtain the solution of the Gompertz growth mo](https://media.cheggcdn.com/media/aba/aba29719-9ff4-42d8-a73e-ebcb557da0c1/php9q3Vf5)