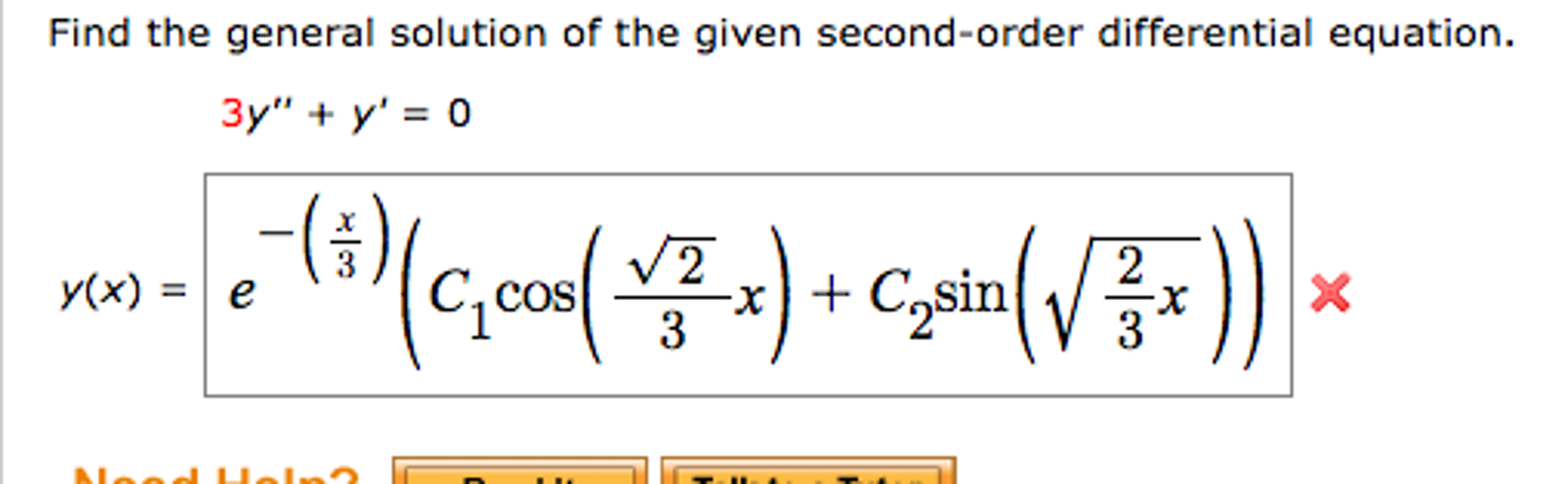General Solution Second Order Differential Equation - In section 2.1 we considered the. Example 5 verify that y 1 = e4x and y. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. Therefore we must be content to solve linear second order equations of special forms. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x.
Therefore we must be content to solve linear second order equations of special forms. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. In section 2.1 we considered the. Example 5 verify that y 1 = e4x and y. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second.
In section 2.1 we considered the. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. Example 5 verify that y 1 = e4x and y. Therefore we must be content to solve linear second order equations of special forms. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x.
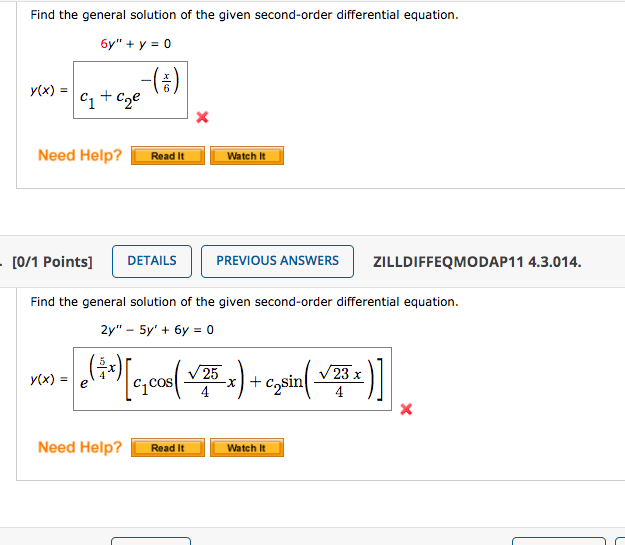
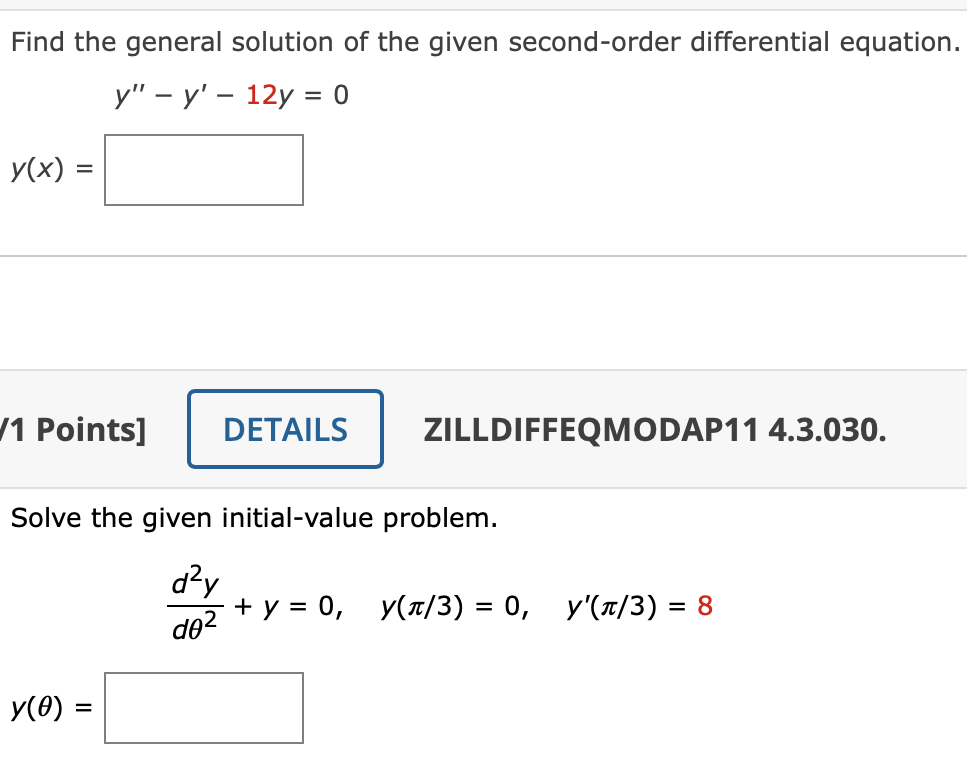
Solved Find the general solution of the given secondorder
Therefore we must be content to solve linear second order equations of special forms. In section 2.1 we considered the. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous.
Solved Find the general solution of the given secondorder
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. Example 5 verify that y 1 = e4x and y. Therefore we must be content to solve linear second order equations of special forms. The functions y 1(x) and y 2(x) are linearly independent if one is not.
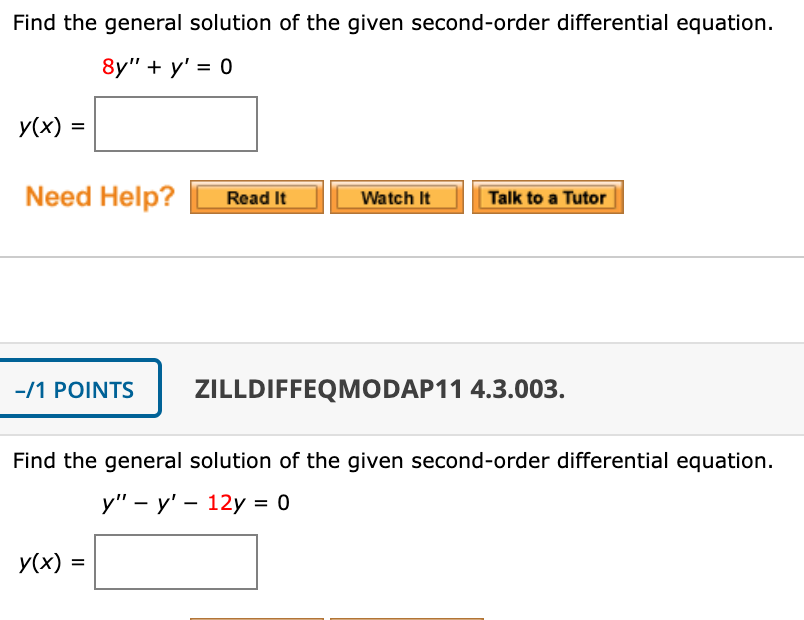
Solved Find the general solution of the given secondorder
The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. In section 2.1 we considered the. Example 5 verify that.
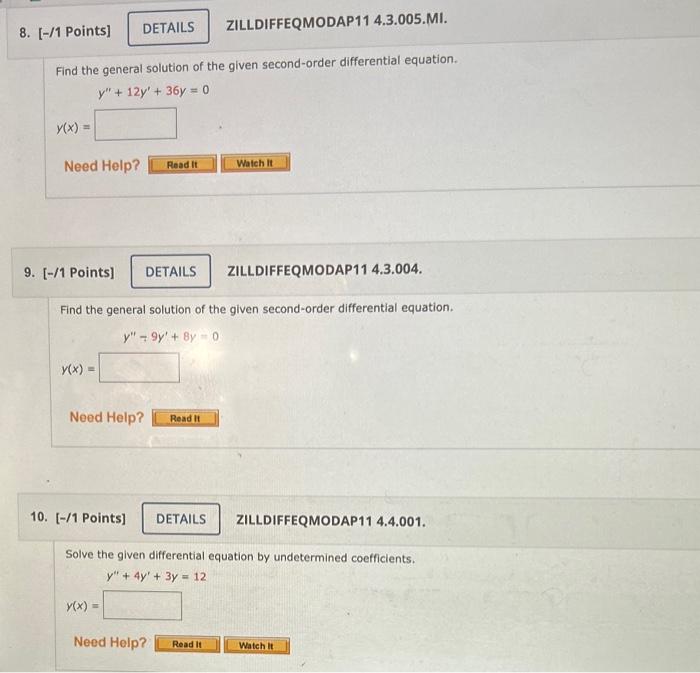
Solved Find the general solution of the given secondorder
Example 5 verify that y 1 = e4x and y. In section 2.1 we considered the. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. Therefore we must be content to solve linear second order equations of special forms. We define fundamental sets of solutions and discuss how they can.
Solved Find the general solution of the given secondorder
Example 5 verify that y 1 = e4x and y. Therefore we must be content to solve linear second order equations of special forms. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. We define fundamental sets of solutions and discuss how they can be used to get a general.
Solved Find the general solution of the following second
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. We define fundamental sets of solutions and discuss how they.
[Solved] . A secondorder differential equation and its general
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. Therefore we must be content to solve linear second order.
Solved Find the general solution of the given secondorder
Example 5 verify that y 1 = e4x and y. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other..
Solved Find the general solution of the given secondorder
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. In section 2.1 we considered the. Example 5 verify that y 1 = e4x and y. Therefore we must be content to solve linear second order equations of special forms. Generally, we write a second order differential equation.
[Solved] The general solution to the secondorder differential equation
Therefore we must be content to solve linear second order equations of special forms. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. In section 2.1 we considered the. Example 5 verify that y 1 = e4x and y. Generally, we write a second order differential equation as y'' +.
Therefore We Must Be Content To Solve Linear Second Order Equations Of Special Forms.
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. The functions y 1(x) and y 2(x) are linearly independent if one is not a multiple of the other. Example 5 verify that y 1 = e4x and y. In section 2.1 we considered the.