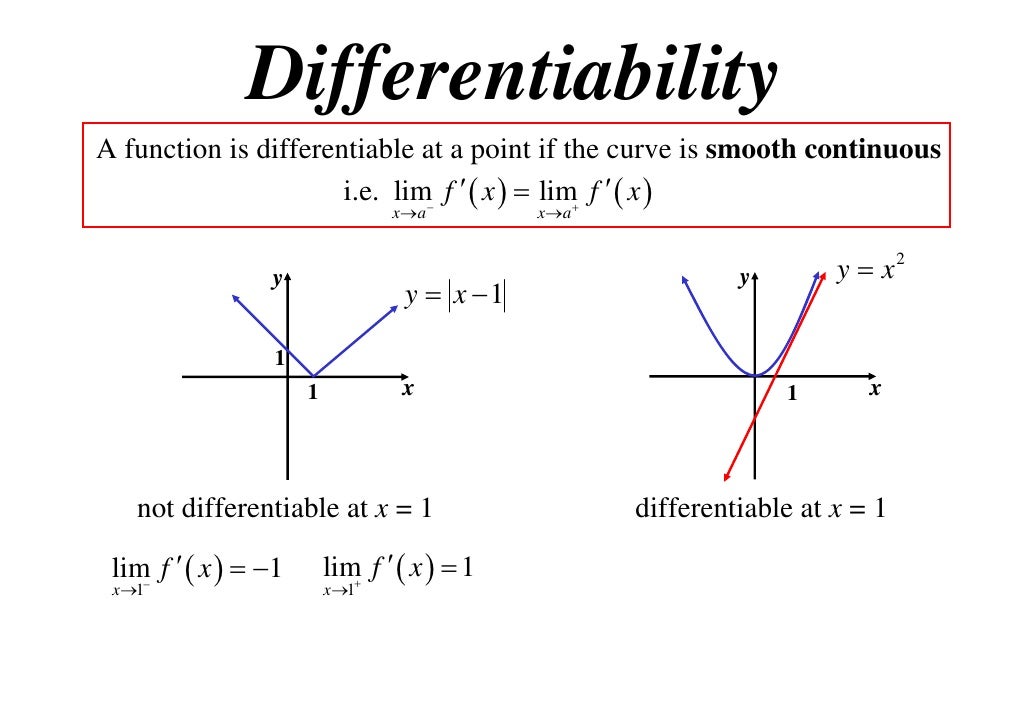
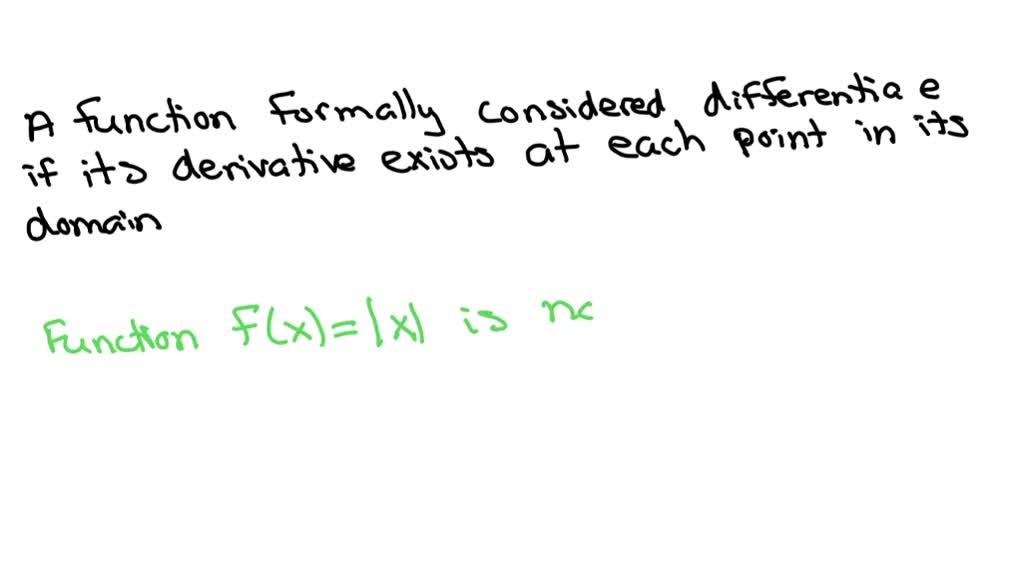Examples Of Not Differentiable - The function jumps at x x, (is not continuous) like. When f is not continuous at x = x 0. Here are a number of cases in which f does not have a derivative at a point. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. For example, if there is a.
The function jumps at x x, (is not continuous) like. Here are a number of cases in which f does not have a derivative at a point. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. When f is not continuous at x = x 0. For example, if there is a.
Here are a number of cases in which f does not have a derivative at a point. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. When f is not continuous at x = x 0. The function jumps at x x, (is not continuous) like. For example, if there is a.
Differentiable Cuemath
Here are a number of cases in which f does not have a derivative at a point. When f is not continuous at x = x 0. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. For example, if there is.
Nondifferentiable functions must have discontinuous partial
For example, if there is a. The function jumps at x x, (is not continuous) like. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. When f is not continuous at x = x 0. Here are a number of cases.
Differentiable Function Meaning, Formulas and Examples Outlier
For example, if there is a. The function jumps at x x, (is not continuous) like. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have a derivative at a.
Nondifferentiable functions must have discontinuous partial
When f is not continuous at x = x 0. Here are a number of cases in which f does not have a derivative at a point. The function jumps at x x, (is not continuous) like. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but.
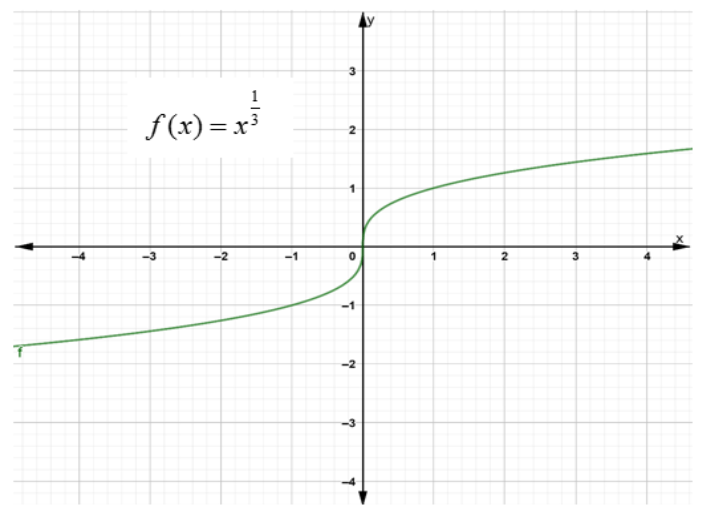
What are some examples of nondifferentiable functions?
For example, if there is a. When f is not continuous at x = x 0. The function jumps at x x, (is not continuous) like. Here are a number of cases in which f does not have a derivative at a point. We can say that f is not differentiable for any value of x where a tangent cannot.
Can Something Be Differentiable but Not Continuous Quant RL
For example, if there is a. When f is not continuous at x = x 0. Here are a number of cases in which f does not have a derivative at a point. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line.
When Is a Function Continuous but Not Differentiable Quant RL
The function jumps at x x, (is not continuous) like. Here are a number of cases in which f does not have a derivative at a point. When f is not continuous at x = x 0. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but.
SOLVEDWrite a paragraph that explains what it means for a function to
The function jumps at x x, (is not continuous) like. Here are a number of cases in which f does not have a derivative at a point. When f is not continuous at x = x 0. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but.
Differentiable vs. Continuous Functions Understanding the Distinctions
Here are a number of cases in which f does not have a derivative at a point. The function jumps at x x, (is not continuous) like. For example, if there is a. When f is not continuous at x = x 0. We can say that f is not differentiable for any value of x where a tangent cannot.
Can Something Be Differentiable but Not Continuous Quant RL
When f is not continuous at x = x 0. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have a derivative at a point. For example, if there is.
When F Is Not Continuous At X = X 0.
The function jumps at x x, (is not continuous) like. We can say that f is not differentiable for any value of x where a tangent cannot 'exist' or the tangent exists but is vertical (vertical line has. Here are a number of cases in which f does not have a derivative at a point. For example, if there is a.