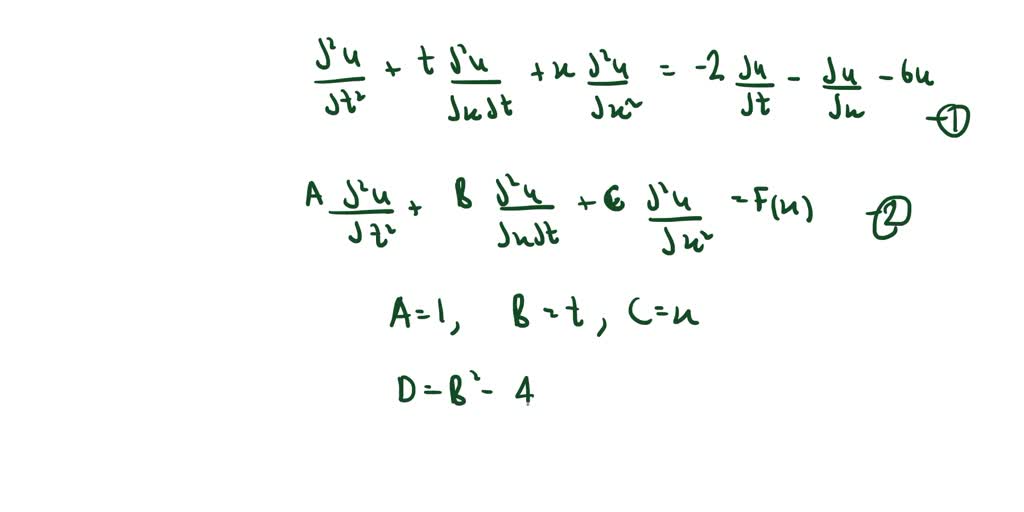Elliptic Differential Equation - This could model the temperature distribution on a square floor. A solution to this equation is u(x; Elliptic partial differential equations by qing. Differential operator of one of the two forms: Lu= xn i,j=1 a ij(x)∂ iju(a non. Primarily the dirichlet problem for various types of elliptic equations. Thus, the laplace equation is elliptic. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Praise for the first edition:
A solution to this equation is u(x; This could model the temperature distribution on a square floor. Elliptic partial differential equations by qing. Differential operator of one of the two forms: Thus, the laplace equation is elliptic. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Lu= xn i,j=1 a ij(x)∂ iju(a non. Praise for the first edition: Primarily the dirichlet problem for various types of elliptic equations.
Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. This could model the temperature distribution on a square floor. Lu= xn i,j=1 a ij(x)∂ iju(a non. A solution to this equation is u(x; Elliptic partial differential equations by qing. Thus, the laplace equation is elliptic. Differential operator of one of the two forms: Primarily the dirichlet problem for various types of elliptic equations. Praise for the first edition:
MAFE208IUL14 Elliptic Equation PDF Partial Differential Equation
This could model the temperature distribution on a square floor. Elliptic partial differential equations by qing. Differential operator of one of the two forms: A solution to this equation is u(x; Lu= xn i,j=1 a ij(x)∂ iju(a non.
(PDF) Analytic regularity and solution approximation for a semilinear
Primarily the dirichlet problem for various types of elliptic equations. Praise for the first edition: Lu= xn i,j=1 a ij(x)∂ iju(a non. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Differential operator of one of the two forms:
Solved Solve the elliptic partial differential equation
Elliptic partial differential equations by qing. Lu= xn i,j=1 a ij(x)∂ iju(a non. Primarily the dirichlet problem for various types of elliptic equations. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. A solution to this equation is u(x;
Lecture 7_elliptic partial differential equation PDF Equations
Elliptic partial differential equations by qing. A solution to this equation is u(x; Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Differential operator of one of the two forms: This could model the temperature distribution on a square floor.
Finalchapter4part4 Pde Elliptic Download Free PDF Partial
This could model the temperature distribution on a square floor. A solution to this equation is u(x; Primarily the dirichlet problem for various types of elliptic equations. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Thus, the laplace equation is elliptic.
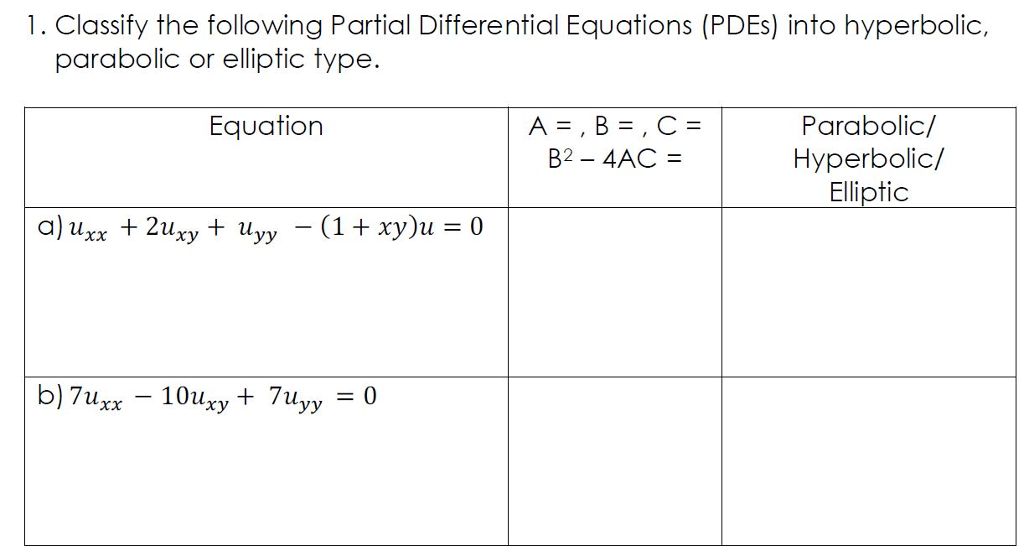
SOLVED Classify the partial differential equation ∂^2u/∂x^2 + 5âˆ
Differential operator of one of the two forms: A solution to this equation is u(x; Elliptic partial differential equations by qing. Primarily the dirichlet problem for various types of elliptic equations. This could model the temperature distribution on a square floor.
Online video course design of elliptic partial differential equation
A solution to this equation is u(x; Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Lu= xn i,j=1 a ij(x)∂ iju(a non. Praise for the first edition: This could model the temperature distribution on a square floor.
Boundary value problems for a secondorder elliptic partial
Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Thus, the laplace equation is elliptic. A solution to this equation is u(x; Differential operator of one of the two forms: Elliptic partial differential equations by qing.
Solved 5. Which type of differential equation is used to
Praise for the first edition: Thus, the laplace equation is elliptic. This could model the temperature distribution on a square floor. Elliptic partial differential equations by qing. Lu= xn i,j=1 a ij(x)∂ iju(a non.
Solved 1. Classify the following Partial Differential
Elliptic partial differential equations by qing. Praise for the first edition: Thus, the laplace equation is elliptic. Lu= xn i,j=1 a ij(x)∂ iju(a non. This could model the temperature distribution on a square floor.
A Solution To This Equation Is U(X;
Differential operator of one of the two forms: Praise for the first edition: Lu= xn i,j=1 a ij(x)∂ iju(a non. Elliptic partial differential equations by qing.
Thus, The Laplace Equation Is Elliptic.
This could model the temperature distribution on a square floor. Primarily the dirichlet problem for various types of elliptic equations. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2.