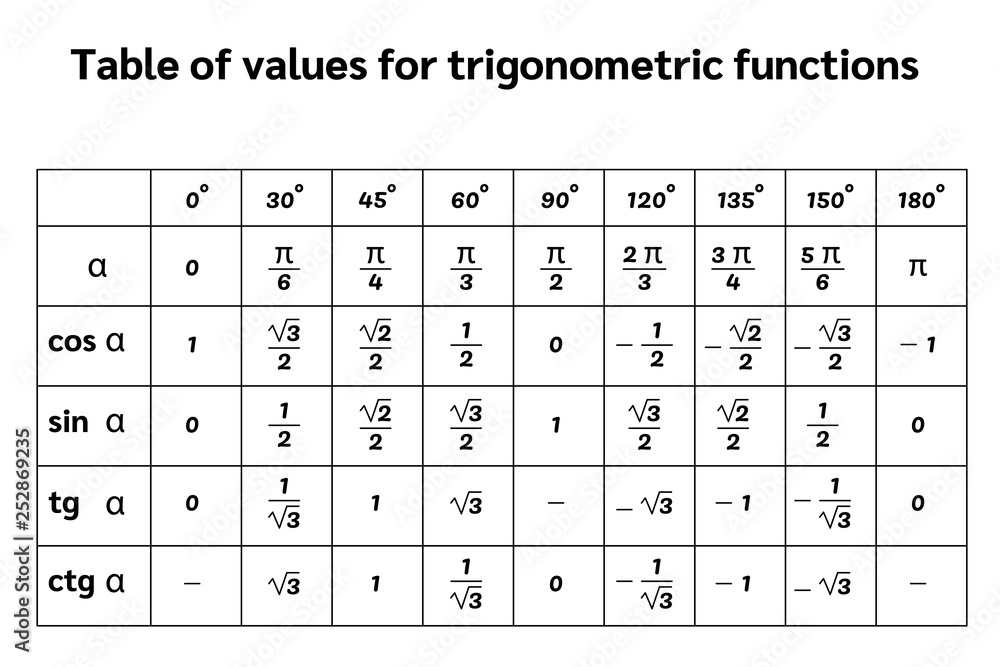
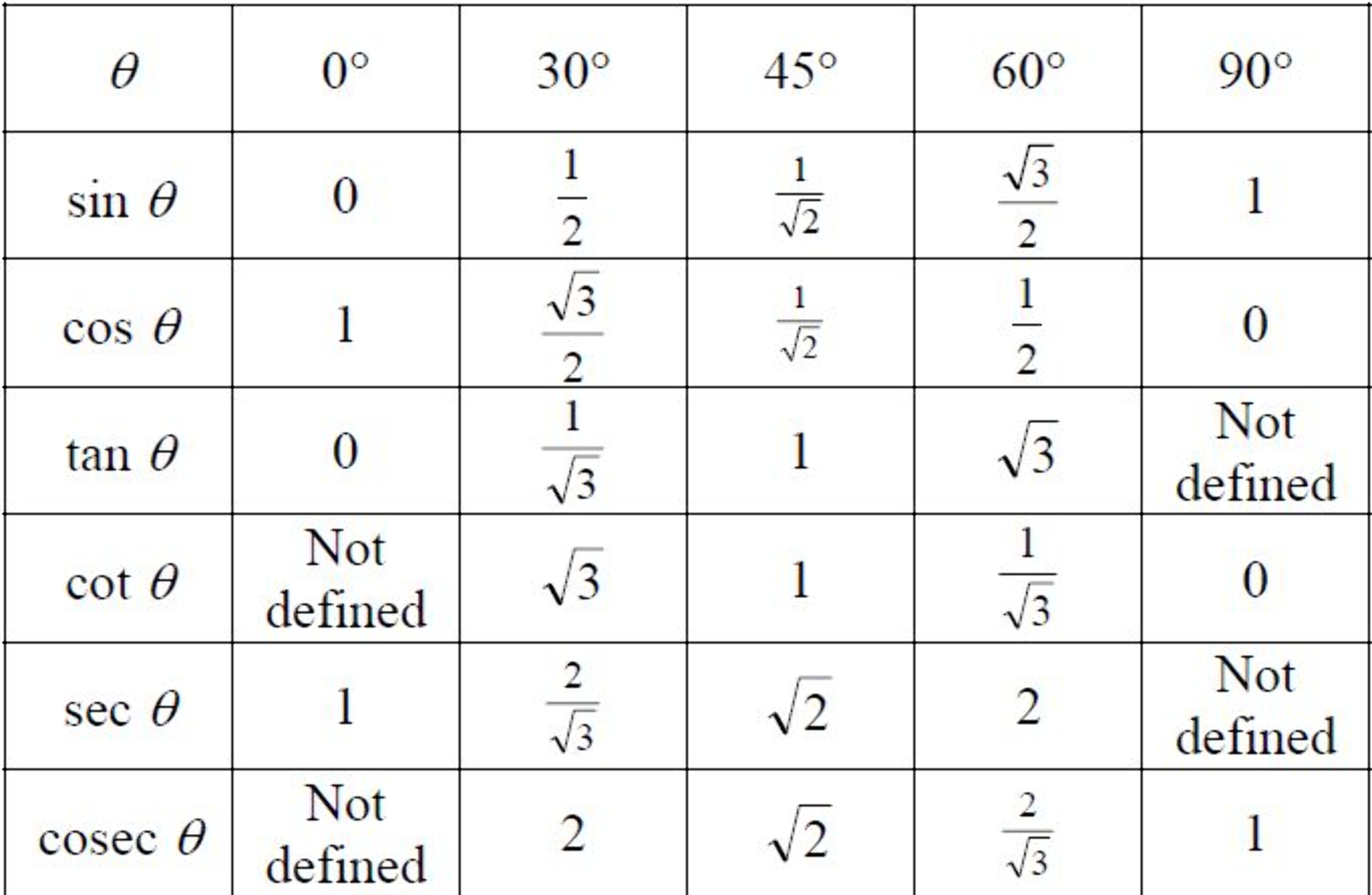
Differentiation Table Trigonometric Functions - The basic trigonometric functions include the following 6 functions: Rules for derivatives rule for addition: Thus we can use the product, quotient and chain rules to differentiate functions that are combinations of the trigonometric functions. Line integral of a vector field; The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec. If h(x) = f(x)+g(x) or d dx (u+v) = du dx + dv dx then h0(x) = f0(x)+g0(x) rule for scalar. Gradient of a scalar function; Line integral of a scalar field; The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change.
Line integral of a scalar field; The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. Gradient of a scalar function; Line integral of a vector field; Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec. Thus we can use the product, quotient and chain rules to differentiate functions that are combinations of the trigonometric functions. If h(x) = f(x)+g(x) or d dx (u+v) = du dx + dv dx then h0(x) = f0(x)+g0(x) rule for scalar. The basic trigonometric functions include the following 6 functions: Divergence of a vector field;. The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change.
The basic trigonometric functions include the following 6 functions: Line integral of a vector field; The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. If h(x) = f(x)+g(x) or d dx (u+v) = du dx + dv dx then h0(x) = f0(x)+g0(x) rule for scalar. Line integral of a scalar field; Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec. Rules for derivatives rule for addition: Gradient of a scalar function; Divergence of a vector field;. The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change.
OMTEX CLASSES Trigonometric Table
Line integral of a vector field; The basic trigonometric functions include the following 6 functions: Line integral of a scalar field; Thus we can use the product, quotient and chain rules to differentiate functions that are combinations of the trigonometric functions. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec.
How to Remember the Trigonometric Table 5 Steps (with Pictures)
The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. Divergence of a vector field;. Gradient of a scalar function; Line integral of a scalar field; Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec.
(PDF) Table of Trigonometric Functions Exact Values for Special Angles
The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. Rules for derivatives rule for addition: Line integral of a scalar field; If h(x) = f(x)+g(x) or d dx (u+v) = du dx + dv dx then h0(x) = f0(x)+g0(x) rule for scalar. Gradient of a scalar function;
Full Table Of Trigonometric Functions at Lucia Erby blog
If h(x) = f(x)+g(x) or d dx (u+v) = du dx + dv dx then h0(x) = f0(x)+g0(x) rule for scalar. Line integral of a scalar field; Line integral of a vector field; Gradient of a scalar function; Rules for derivatives rule for addition:
Trigonometric Ratios Table Radians Review Home Decor
The basic trigonometric functions include the following 6 functions: If h(x) = f(x)+g(x) or d dx (u+v) = du dx + dv dx then h0(x) = f0(x)+g0(x) rule for scalar. Line integral of a vector field; The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. Rules.
Worksheet Trig Derivatives PDF Sine Trigonometric Functions
The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec. Thus we can use the product, quotient and chain rules to differentiate functions that are combinations of the trigonometric functions. The basic trigonometric.
Differentiation of Trigonometric Functions Trig Derivatives
Divergence of a vector field;. The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. If h(x) = f(x)+g(x) or d dx (u+v) = du dx + dv dx then h0(x) = f0(x)+g0(x) rule for scalar. Gradient of a scalar function; Line integral of a vector field;
TABLE OF TRIGONOMETRIC IDENTITIES Math2ever™ place to learn basic
The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. Thus we can use the product, quotient and chain rules to differentiate functions that are combinations of the trigonometric functions. Rules for derivatives rule for addition: If h(x) = f(x)+g(x) or d dx (u+v) = du dx.
black table of trigonometric functions vector illustration Stock Vector
The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. Line integral of a vector field; Rules for derivatives rule for addition: Divergence of a vector field;. Line integral of a scalar field;
Table Of Values For 6 Trigonometric Functions
The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. Line integral of a scalar field; Gradient of a scalar function; The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine,. If h(x) = f(x)+g(x).
Gradient Of A Scalar Function;
Line integral of a scalar field; Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec. The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. If h(x) = f(x)+g(x) or d dx (u+v) = du dx + dv dx then h0(x) = f0(x)+g0(x) rule for scalar.
The Following Table Summarizes The Derivatives Of The Six Trigonometric Functions, As Well As Their Chain Rule Counterparts (That Is, The Sine, Cosine,.
Thus we can use the product, quotient and chain rules to differentiate functions that are combinations of the trigonometric functions. The basic trigonometric functions include the following 6 functions: Rules for derivatives rule for addition: Line integral of a vector field;