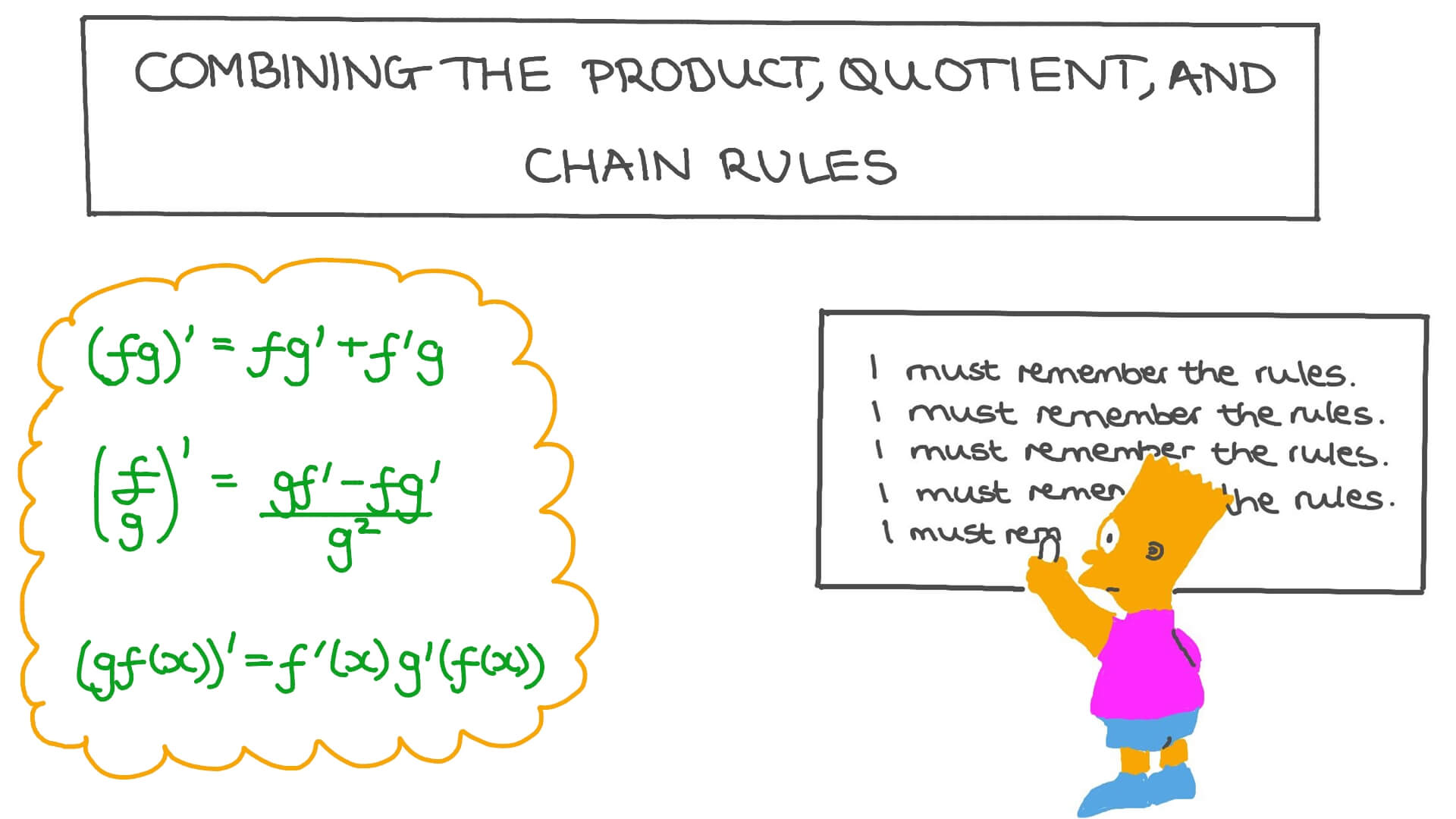
Differentiation Product And Quotient Rule - In this chapter we introduce derivatives. This is another very useful formula: In what follows, f and g are differentiable functions of x. To differentiate products and quotients we have the product rule and the quotient rule. D (uv) = vdu + udv dx dx dx. If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it. The product and quotient rules are covered in this section. D dx(f ⋅ g) = f ′ ⋅ g + f ⋅ g ′. The derivative of the first factor times the. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well.
The product and quotient rules are covered in this section. In this chapter we introduce derivatives. If the two functions \ (f\left ( x. Here is a set of practice problems to accompany the product and quotient rule section of the derivatives chapter of the notes. In what follows, f and g are differentiable functions of x. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well. The sum/difference, constant multiple, power, product and quotient rules show us how to find the derivatives of certain. If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it. D dx(f ⋅ g) = f ′ ⋅ g + f ⋅ g ′. D (uv) = vdu + udv dx dx dx.
In what follows, f and g are differentiable functions of x. This is another very useful formula: Here is a set of practice problems to accompany the product and quotient rule section of the derivatives chapter of the notes. D (uv) = vdu + udv dx dx dx. In this chapter we introduce derivatives. The sum/difference, constant multiple, power, product and quotient rules show us how to find the derivatives of certain. The product and quotient rules are covered in this section. If the two functions \ (f\left ( x. D dx(f ⋅ g) = f ′ ⋅ g + f ⋅ g ′. If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it.
Product And Quotient Rule Worksheet Zip Worksheet
If the two functions \ (f\left ( x. The derivative of the first factor times the. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well. D dx(f ⋅ g) = f ′ ⋅ g + f ⋅ g ′. This is another very useful formula:
Differentiation Product & Quotient Rule Kappa Maths Resources for A
D (uv) = vdu + udv dx dx dx. In what follows, f and g are differentiable functions of x. To differentiate products and quotients we have the product rule and the quotient rule. The derivative of the first factor times the. This is another very useful formula:
A2 Differentiation Quotient Rule Part 1 alevelmathematicsnotes
Here is a set of practice problems to accompany the product and quotient rule section of the derivatives chapter of the notes. D (uv) = vdu + udv dx dx dx. In this chapter we introduce derivatives. D dx(f ⋅ g) = f ′ ⋅ g + f ⋅ g ′. This is another very useful formula:
Differentiation Product & Quotient Rule Kappa Maths Resources for A
The product and quotient rules are covered in this section. D dx(f ⋅ g) = f ′ ⋅ g + f ⋅ g ′. The derivative of the first factor times the. If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it. To differentiate products.
Differentiation Product & Quotient Rule Kappa Maths Resources for A
This is another very useful formula: In this chapter we introduce derivatives. If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it. If the two functions \ (f\left ( x. The derivative of the first factor times the.
Products, Quotients, and Chains Simple Rules for Calculus
The sum/difference, constant multiple, power, product and quotient rules show us how to find the derivatives of certain. To differentiate products and quotients we have the product rule and the quotient rule. The derivative of the first factor times the. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well. D (uv) =.
A2 Differentiation Quotient Rule Part 1 alevelmathematicsnotes
If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it. Here is a set of practice problems to accompany the product and quotient rule section of the derivatives chapter of the notes. In what follows, f and g are differentiable functions of x. In this.
Product And Quotient Rule Worksheet Zip Worksheet
If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well. Here is a set of practice problems to accompany the product and quotient rule section of the derivatives.
Product And Quotient Rule Worksheet Zip Worksheet
To differentiate products and quotients we have the product rule and the quotient rule. D (uv) = vdu + udv dx dx dx. If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it. The product and quotient rules are covered in this section. In what.
Differentiation Product & Quotient Rule Kappa Maths Resources for A
This is another very useful formula: To differentiate products and quotients we have the product rule and the quotient rule. In what follows, f and g are differentiable functions of x. If the two functions \ (f\left ( x. Here is a set of practice problems to accompany the product and quotient rule section of the derivatives chapter of the.
In What Follows, F And G Are Differentiable Functions Of X.
If a function is a sum, product, or quotient of simpler functions, then we can use the sum, product, or quotient rules to differentiate it. The derivative of the first factor times the. We cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well. This is another very useful formula:
Here Is A Set Of Practice Problems To Accompany The Product And Quotient Rule Section Of The Derivatives Chapter Of The Notes.
If the two functions \ (f\left ( x. The sum/difference, constant multiple, power, product and quotient rules show us how to find the derivatives of certain. D (uv) = vdu + udv dx dx dx. The product and quotient rules are covered in this section.
In This Chapter We Introduce Derivatives.
D dx(f ⋅ g) = f ′ ⋅ g + f ⋅ g ′. To differentiate products and quotients we have the product rule and the quotient rule.