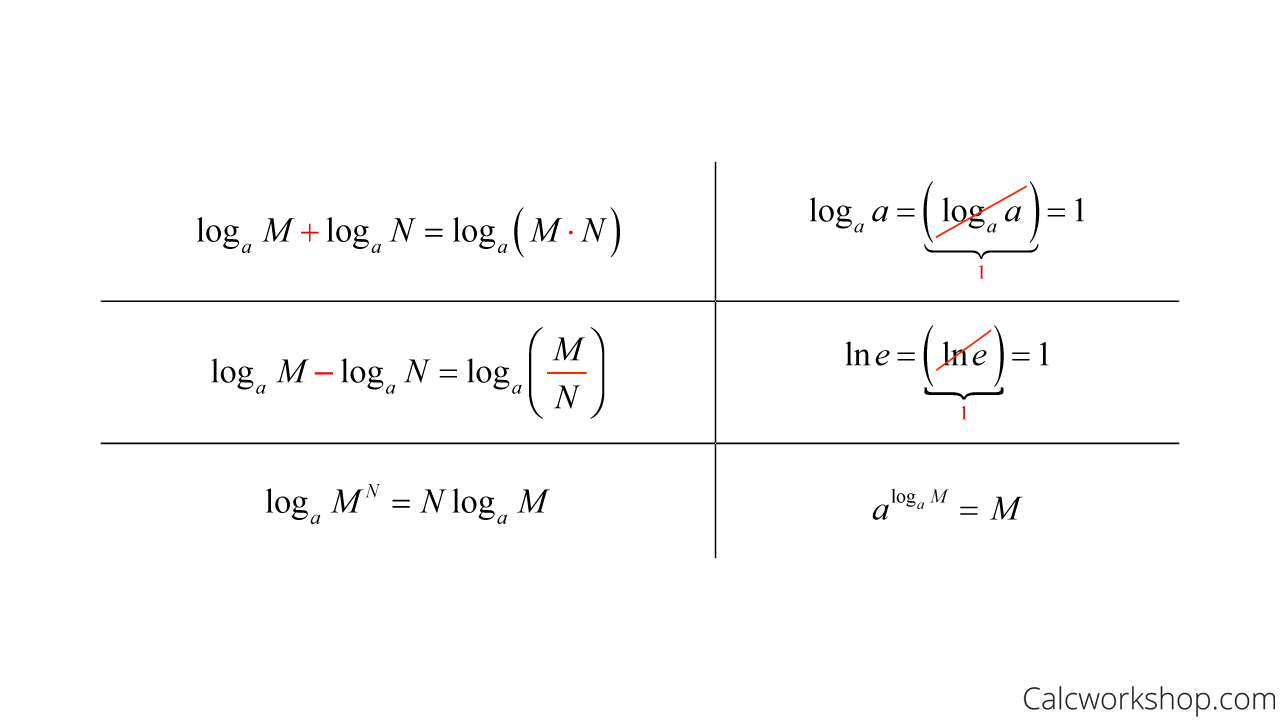
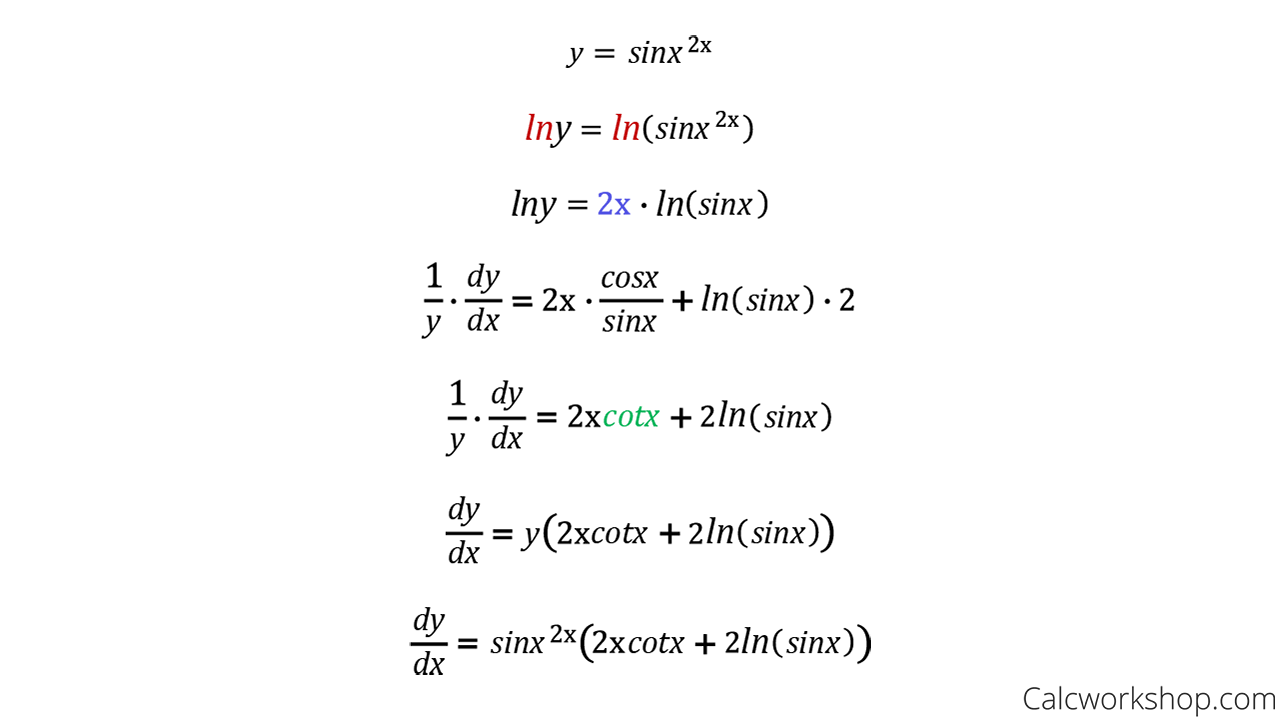
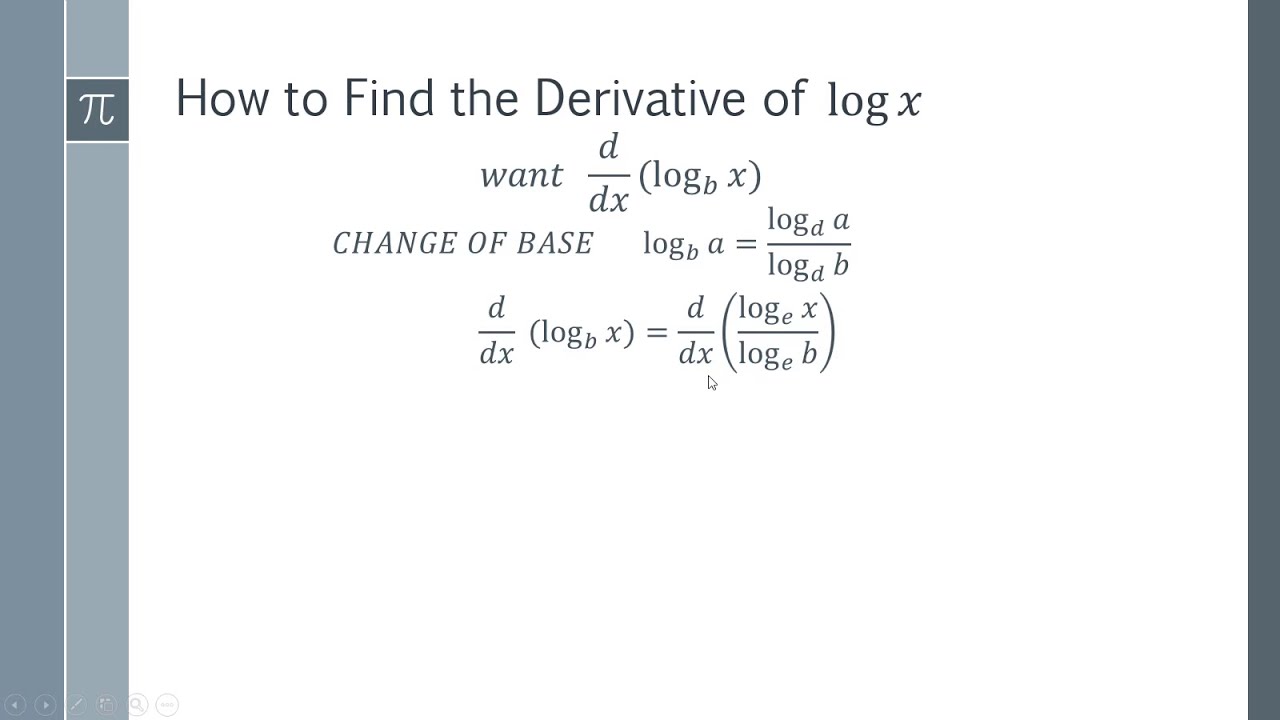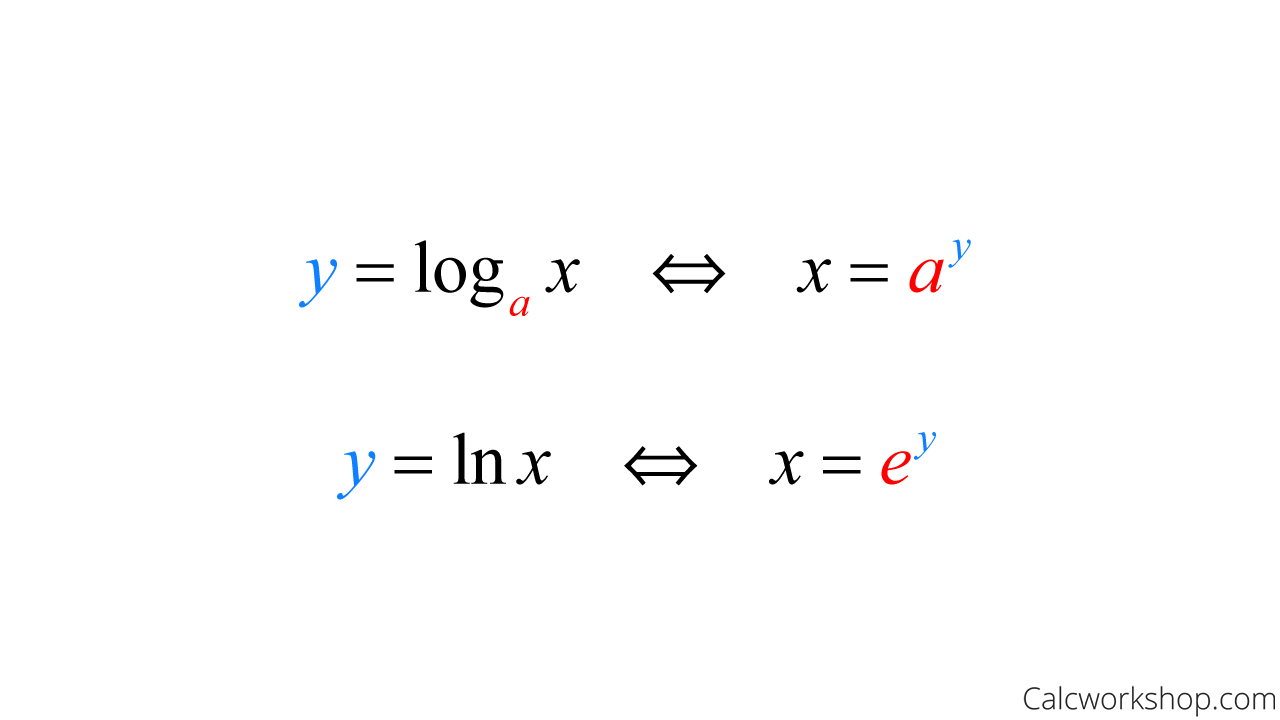Differentiation Of Log E - Log e is made up of two terms log and e where log is a logarithm function, where one number is raised on the power of another. According to the properties to the logarithmic function, the value of log e e is given as 1. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. In this booklet we will use both these notations. We can use these results and the rules that we have learnt already to differentiate functions. Therefore, loge e = 1 (or) ln (e)= 1.
In this booklet we will use both these notations. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. According to the properties to the logarithmic function, the value of log e e is given as 1. We can use these results and the rules that we have learnt already to differentiate functions. Therefore, loge e = 1 (or) ln (e)= 1. Log e is made up of two terms log and e where log is a logarithm function, where one number is raised on the power of another.
In this booklet we will use both these notations. Log e is made up of two terms log and e where log is a logarithm function, where one number is raised on the power of another. Therefore, loge e = 1 (or) ln (e)= 1. We can use these results and the rules that we have learnt already to differentiate functions. According to the properties to the logarithmic function, the value of log e e is given as 1. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by.
Differentiation eMaths.ie
Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Log e is made up of two terms log and e where log is a logarithm function, where one number is raised on the power of another. Therefore, loge e = 1 (or) ln (e)= 1. We can use these results and the rules.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
Therefore, loge e = 1 (or) ln (e)= 1. According to the properties to the logarithmic function, the value of log e e is given as 1. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. We can use these results and the rules that we have learnt already to differentiate functions. Log.
7 Differentiation of ( log _ { mathrm { e } } mathrm { x } ) w
According to the properties to the logarithmic function, the value of log e e is given as 1. We can use these results and the rules that we have learnt already to differentiate functions. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Therefore, loge e = 1 (or) ln (e)= 1. In.
Differentiation Of Log X
In this booklet we will use both these notations. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Log e is made up of two terms log and e where log is a logarithm function, where one number is raised on the power of another. We can use these results and the rules.
Differentiation Of Log X
Log e is made up of two terms log and e where log is a logarithm function, where one number is raised on the power of another. In this booklet we will use both these notations. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. According to the properties to the logarithmic function,.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
According to the properties to the logarithmic function, the value of log e e is given as 1. Therefore, loge e = 1 (or) ln (e)= 1. We can use these results and the rules that we have learnt already to differentiate functions. Log e is made up of two terms log and e where log is a logarithm function,.
Log Y Differentiation at Jeremy Broady blog
We can use these results and the rules that we have learnt already to differentiate functions. In this booklet we will use both these notations. Therefore, loge e = 1 (or) ln (e)= 1. According to the properties to the logarithmic function, the value of log e e is given as 1. Log e is made up of two terms.
Differentiation Of Log X
Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. According to the properties to the logarithmic function, the value of log e e is given as 1. Therefore, loge e = 1 (or) ln (e)= 1. In this booklet we will use both these notations. We can use these results and the rules.
Differentiation Of Log X
We can use these results and the rules that we have learnt already to differentiate functions. According to the properties to the logarithmic function, the value of log e e is given as 1. In this booklet we will use both these notations. Therefore, loge e = 1 (or) ln (e)= 1. Logarithmic differentiation allows us to differentiate functions of.
Differentiation Rules
In this booklet we will use both these notations. Log e is made up of two terms log and e where log is a logarithm function, where one number is raised on the power of another. Therefore, loge e = 1 (or) ln (e)= 1. According to the properties to the logarithmic function, the value of log e e is.
Therefore, Loge E = 1 (Or) Ln (E)= 1.
In this booklet we will use both these notations. We can use these results and the rules that we have learnt already to differentiate functions. Log e is made up of two terms log and e where log is a logarithm function, where one number is raised on the power of another. According to the properties to the logarithmic function, the value of log e e is given as 1.