Differentiation Of Dot Product - In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. Taking the derivative of this object is just using the. | | v | | 2 = v ⋅ v. The proof can be extended to any kind of dot product defined. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. The dot product of $\mathbf f$ with its derivative is given by: $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =.
Taking the derivative of this object is just using the. The proof can be extended to any kind of dot product defined. $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. The dot product of $\mathbf f$ with its derivative is given by: | | v | | 2 = v ⋅ v. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v.
$\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. Taking the derivative of this object is just using the. The proof can be extended to any kind of dot product defined. | | v | | 2 = v ⋅ v. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. The dot product of $\mathbf f$ with its derivative is given by: In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v.
The Comprehensive Guide to Understanding Dot Products The Knowledge Hub
$\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. The proof can be extended to any kind of dot product defined. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. Taking the derivative of this object is just using the. The dot product of $\mathbf f$ with its derivative.
Product Differentiation Curves
In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. The proof can be extended to any kind of dot product defined. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. | | v | | 2 = v ⋅ v. Taking the derivative of this object is.
The Comprehensive Guide to Understanding Dot Products The Knowledge Hub
$\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. The proof can be extended to any kind of dot product defined. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. | | v | | 2 = v ⋅ v. The dot product of $\mathbf f$ with its.
Dot Product Calculator The Mathematics Master
| | v | | 2 = v ⋅ v. The proof can be extended to any kind of dot product defined. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. $\map {\mathbf f} x \cdot \dfrac {\map.
Product Differentiation 101
$\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. | | v | | 2 = v ⋅ v. Taking the derivative of this object is just using the. The dot product of $\mathbf f$ with its derivative is given by: In fact, recall that for a vector v v, we have that ||v||2 =v.
Dot Product dan cross product PDF
The dot product of $\mathbf f$ with its derivative is given by: In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. Taking the derivative of this object is just using the. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. | | v | | 2 =.
Write a Note on Product Differentiation MBA Notesworld
You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. The dot product of $\mathbf f$ with its derivative is given by: The proof can be extended to any kind of dot product defined. $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. | | v | | 2.
Dot Product After1995
The proof can be extended to any kind of dot product defined. Taking the derivative of this object is just using the. | | v | | 2 = v ⋅ v. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. The dot product of $\mathbf f$ with its derivative is given by:
The Dot Product Definition and Example Math lab, Algebra, Mathematics
You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. The dot product of $\mathbf f$ with its derivative is given by: In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. Taking the derivative of this object is just using the. The proof can be extended to any.
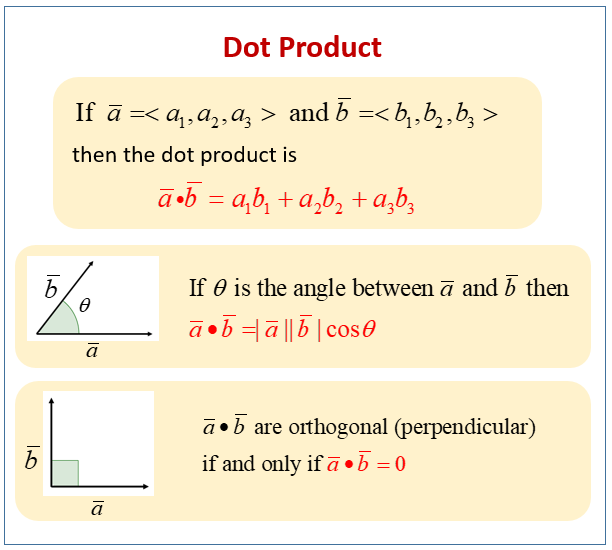
The Dot Product (solutions, examples, videos)
The proof can be extended to any kind of dot product defined. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. The dot product of $\mathbf f$ with its derivative is given by: | | v | |.
In Fact, Recall That For A Vector V V, We Have That ||V||2 =V ⋅V.
| | v | | 2 = v ⋅ v. The dot product of $\mathbf f$ with its derivative is given by: $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +.
Taking The Derivative Of This Object Is Just Using The.
The proof can be extended to any kind of dot product defined.