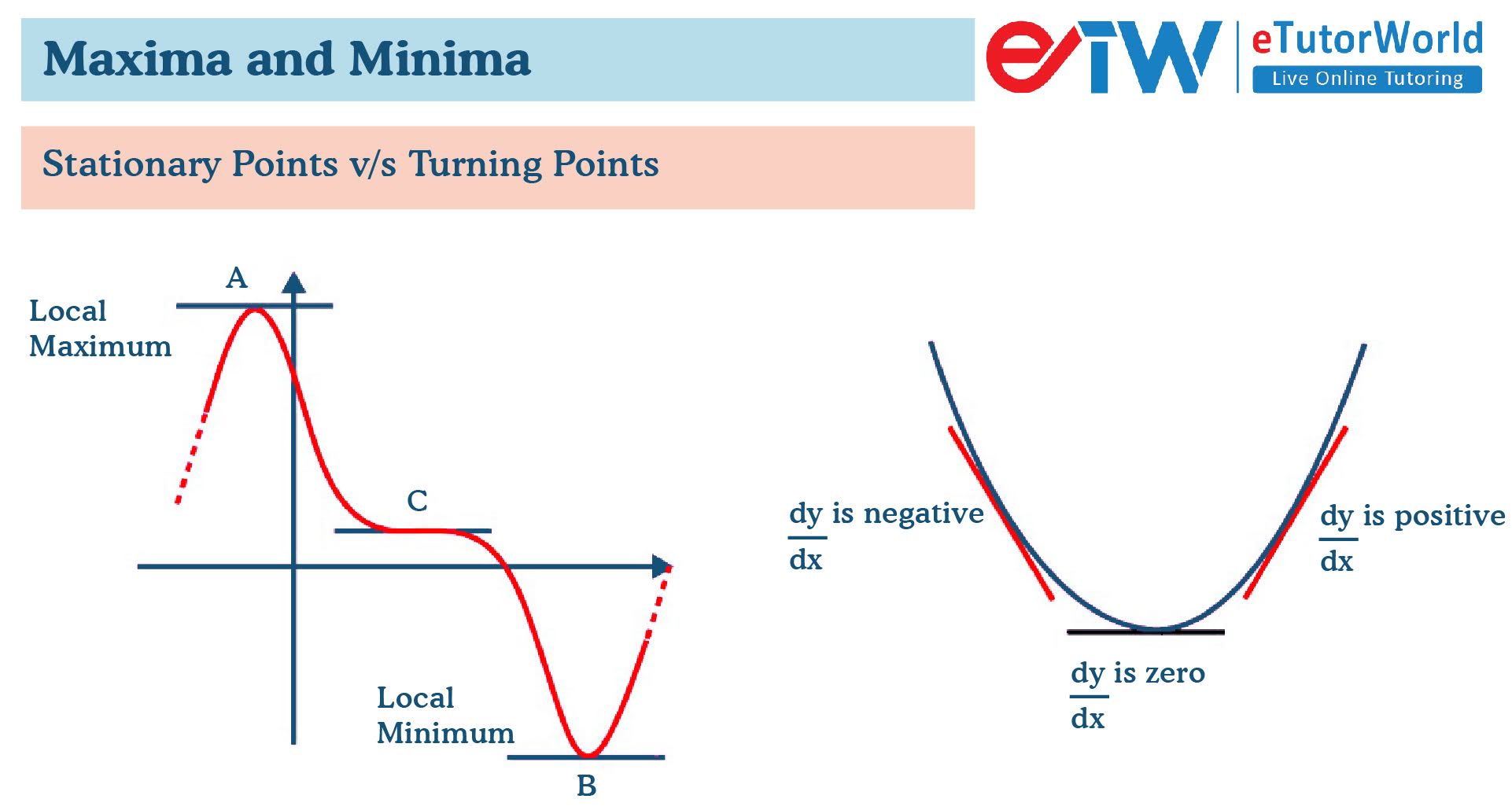
Differentiation Maxima And Minima - Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
SOLUTION Differentiation maxima and minima exam questions Studypool
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Maxima and Minima Definition, Types, Graph, Examples
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Differentiation Maxima and Minima Exam Questions PDF
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Differentiation and Maxima, Minima PDF
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Maxima and Minima Definition, Types, Graph, Examples
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Maxima and Minima Formula, Solved Examples, & FAQs
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
4 Maxima and Minima Download Scientific Diagram
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Differentiation & Maxima & Minima Download Free PDF Maxima And
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Application of Differentiation Maxima and minima 171. If x=t3+t2+t+1, fin..
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.
Chapter 4 Applications of Differentiation PDF Maxima And Minima
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two.