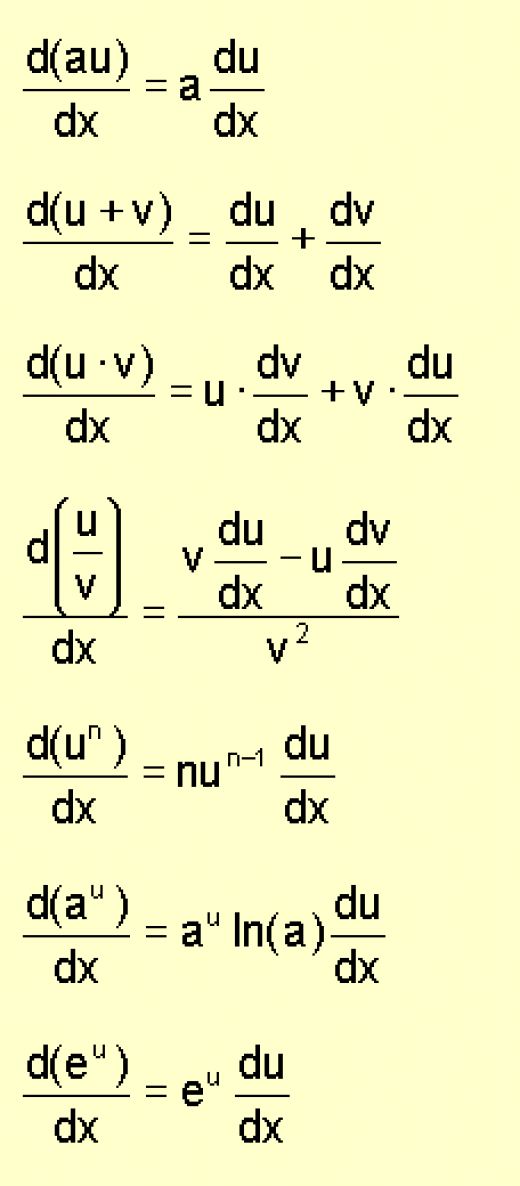Differentiation Integral - As stated above, the basic. We integrate over x and are left with something that depends only on t, not x. Differentiation and integration are branches of calculus where we determine the derivative and integral of a function. Although integration has been introduced as an antiderivative, the symbol for integration is ‘’. For an integral of the form $$\tag{1}\int_a^{g(x)} f(t)\,dt,$$ you would find the derivative using the chain rule. In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a. So to integrate a function f(x),. Under fairly loose conditions on the. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. T) dx is a function of t, so we can ask about its t.
Although integration has been introduced as an antiderivative, the symbol for integration is ‘’. Differentiation and integration are branches of calculus where we determine the derivative and integral of a function. T) dx is a function of t, so we can ask about its t. Under fairly loose conditions on the. We integrate over x and are left with something that depends only on t, not x. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a. As stated above, the basic. So to integrate a function f(x),. For an integral of the form $$\tag{1}\int_a^{g(x)} f(t)\,dt,$$ you would find the derivative using the chain rule.
As stated above, the basic. Under fairly loose conditions on the. Although integration has been introduced as an antiderivative, the symbol for integration is ‘’. T) dx is a function of t, so we can ask about its t. We integrate over x and are left with something that depends only on t, not x. In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a. So to integrate a function f(x),. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Differentiation and integration are branches of calculus where we determine the derivative and integral of a function. For an integral of the form $$\tag{1}\int_a^{g(x)} f(t)\,dt,$$ you would find the derivative using the chain rule.
SOLUTION Differentiation integral rules Studypool
In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a. Under fairly loose conditions on the. T) dx is a function of t, so we can ask about its t. So to integrate a function f(x),. As stated above, the basic.
SOLUTION Differentiation integral formulas Studypool
Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. We integrate over x and are left with something that depends only on t, not x. For an integral of the form $$\tag{1}\int_a^{g(x)} f(t)\,dt,$$ you would find the derivative using the chain rule. Differentiation and integration are branches of calculus where we determine the derivative.
Maths Tips and Tricks INDEFINITE INTEGRAL , DIFFERENTIATION , DEFINITE
T) dx is a function of t, so we can ask about its t. In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a. Although integration has been introduced as an antiderivative, the symbol for integration is ‘’. For an integral of the form $$\tag{1}\int_a^{g(x)} f(t)\,dt,$$ you would find.
SOLUTION Differentiation under integral sign Studypool
Differentiation and integration are branches of calculus where we determine the derivative and integral of a function. In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a. As stated above, the basic. Although integration has been introduced as an antiderivative, the symbol for integration is ‘’. Under fairly loose.
Maths Tips and Tricks INDEFINITE INTEGRAL , DIFFERENTIATION , DEFINITE
As stated above, the basic. So to integrate a function f(x),. We integrate over x and are left with something that depends only on t, not x. T) dx is a function of t, so we can ask about its t. Differentiation and integration are branches of calculus where we determine the derivative and integral of a function.
Differentiation & Integration Integral Life
Although integration has been introduced as an antiderivative, the symbol for integration is ‘’. Under fairly loose conditions on the. As stated above, the basic. T) dx is a function of t, so we can ask about its t. Differentiation and integration are branches of calculus where we determine the derivative and integral of a function.
SOLUTION Differentiation integral formulas Studypool
In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. We integrate over x and are left with something that depends only on t, not x. Under fairly loose conditions on the. Although integration.
Maths Tips and Tricks INDEFINITE INTEGRAL , DIFFERENTIATION , DEFINITE
In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a. Although integration has been introduced as an antiderivative, the symbol for integration is ‘’. As stated above, the basic. Under fairly loose conditions on the. Differentiation under the integral sign is an operation in calculus used to evaluate certain.
SOLUTION Differentiation integral rules Studypool
So to integrate a function f(x),. We integrate over x and are left with something that depends only on t, not x. Under fairly loose conditions on the. As stated above, the basic. Differentiation and integration are branches of calculus where we determine the derivative and integral of a function.
SOLUTION Differentiation under integral sign Studypool
Differentiation and integration are branches of calculus where we determine the derivative and integral of a function. For an integral of the form $$\tag{1}\int_a^{g(x)} f(t)\,dt,$$ you would find the derivative using the chain rule. We integrate over x and are left with something that depends only on t, not x. So to integrate a function f(x),. In mathematics, the problem.
As Stated Above, The Basic.
Differentiation and integration are branches of calculus where we determine the derivative and integral of a function. We integrate over x and are left with something that depends only on t, not x. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. In mathematics, the problem of differentiation of integrals is that of determining under what circumstances the mean value integral of a.
For An Integral Of The Form $$\Tag{1}\Int_A^{G(X)} F(T)\,Dt,$$ You Would Find The Derivative Using The Chain Rule.
Under fairly loose conditions on the. T) dx is a function of t, so we can ask about its t. So to integrate a function f(x),. Although integration has been introduced as an antiderivative, the symbol for integration is ‘’.