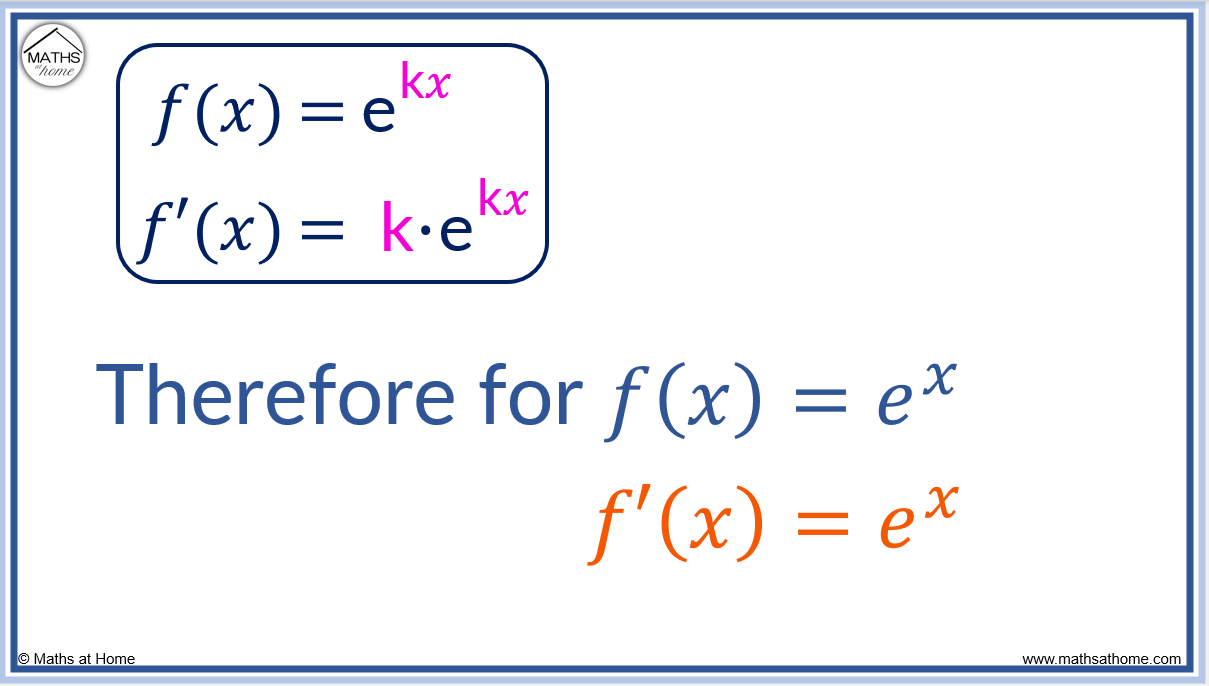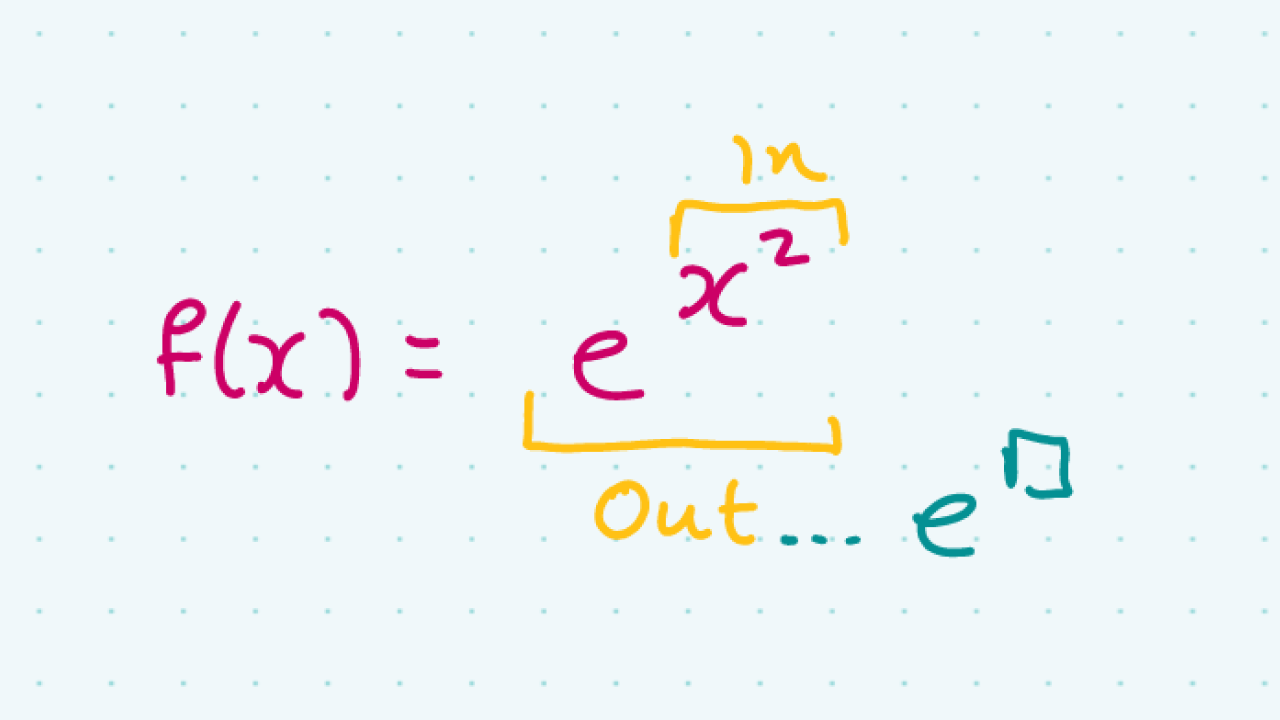Differentiation Exponential Functions - In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. Let's see what happens when we try.
Let's see what happens when we try. The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function.
Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. Let's see what happens when we try.
How to Differentiate Exponential Functions
Let's see what happens when we try. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. Let \(a \gt 0\) and set \(f(x) = a^x\).
How to Differentiate Exponential Functions
Let's see what happens when we try. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. The most common exponential and logarithm functions in.
Exponential Functions Algebra 2 Worksheet Function Worksheets
Let's see what happens when we try. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. The most common exponential and logarithm functions in.
How to Differentiate Exponential Functions
Let's see what happens when we try. The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as.
Differentiation Exponential and Logarithm
Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. Let's see what happens when we try. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as.
PPT Differentiation of Exponential Functions PowerPoint Presentation
Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. The most common exponential and logarithm functions in a calculus course are the natural exponential.
Differentiation exponential functions by MLPTimmins Issuu
In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. The most common exponential and logarithm functions in a calculus course are the natural exponential.
Differentiating Exponential Functions Studyclix
In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as.
PPT 5.4 Exponential Functions Differentiation and Integration
Let's see what happens when we try. The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. Let \(a \gt 0\) and set \(f(x) = a^x\).
PPT 5.4 Exponential Functions Differentiation and Integration
Let's see what happens when we try. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. In order to differentiate the exponential function \[f(x) = a^x,\] we cannot use power rule as we require the exponent to be a fixed number and. The most common exponential and logarithm functions in.
In Order To Differentiate The Exponential Function \[F(X) = A^x,\] We Cannot Use Power Rule As We Require The Exponent To Be A Fixed Number And.
The most common exponential and logarithm functions in a calculus course are the natural exponential function, \({{\bf{e}}^x}\), and. Let \(a \gt 0\) and set \(f(x) = a^x\) — this is what is known as an exponential function. Let's see what happens when we try.