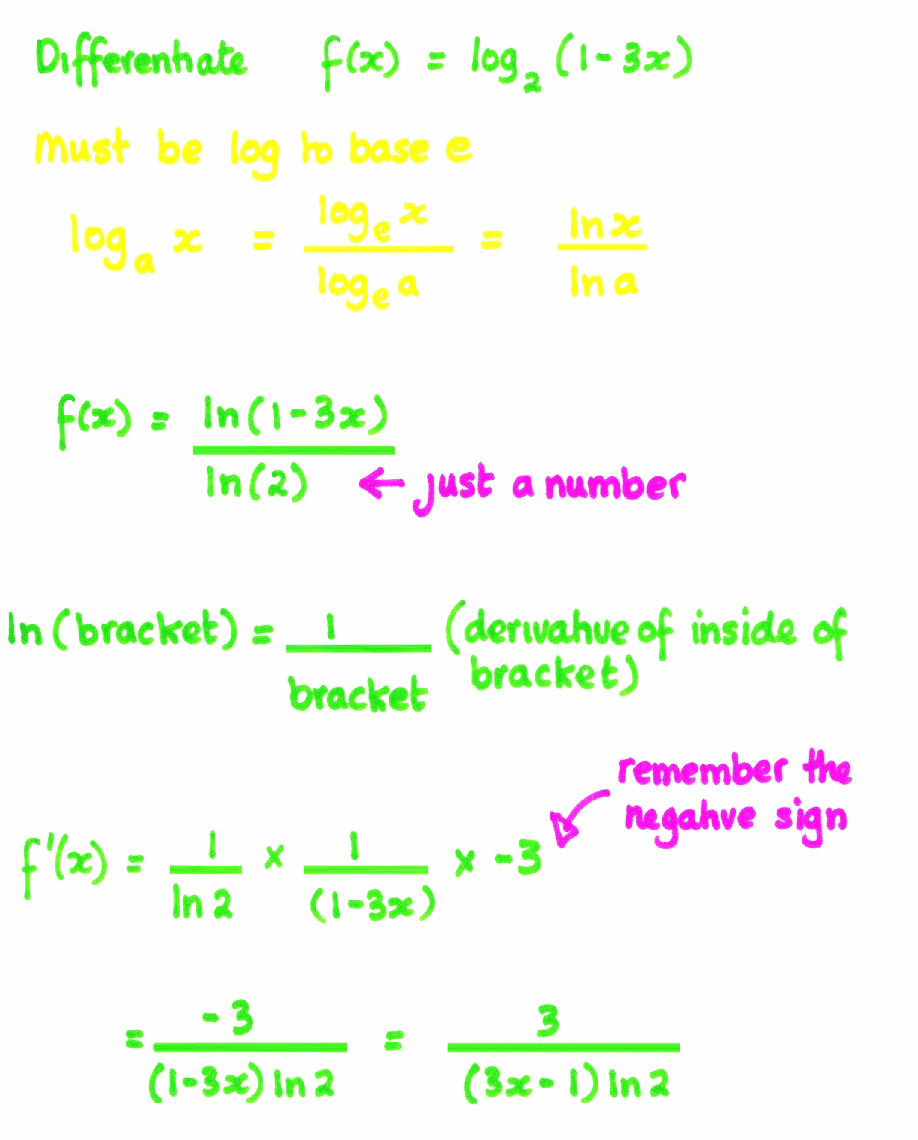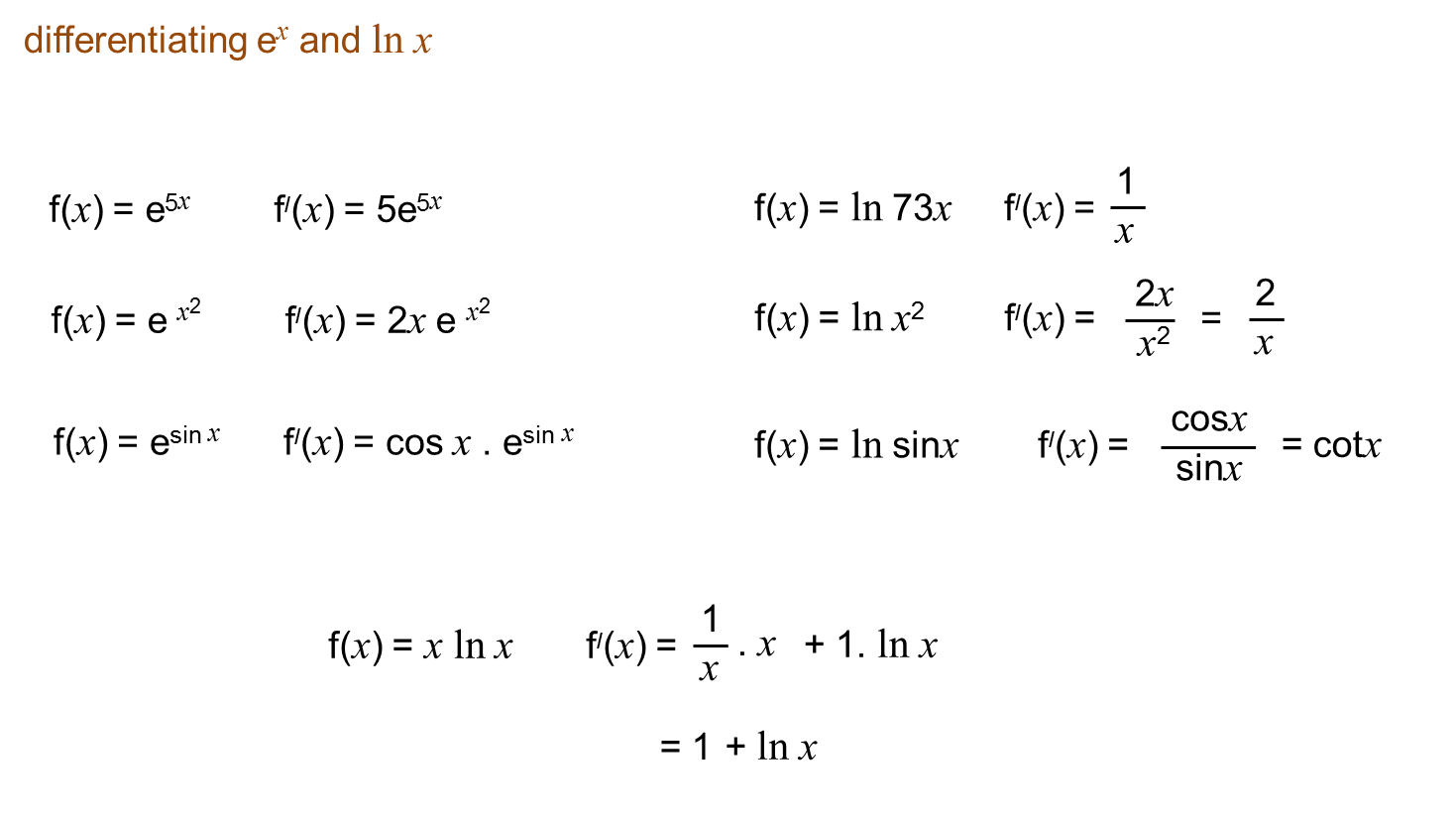Differentiating Logs - Derivatives of logarithmic functions are mainly based on the chain rule. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend. However, we can generalize it for any differentiable function with.
We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend. Derivatives of logarithmic functions are mainly based on the chain rule. However, we can generalize it for any differentiable function with.
We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend. However, we can generalize it for any differentiable function with. Derivatives of logarithmic functions are mainly based on the chain rule.
12X1 T01 02 differentiating logs
However, we can generalize it for any differentiable function with. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend. Derivatives of logarithmic functions are mainly based on the chain rule.
12X1 T01 02 differentiating logs
Derivatives of logarithmic functions are mainly based on the chain rule. However, we can generalize it for any differentiable function with. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend.
CALCULUS Differentiating Natural Logs YouTube
Derivatives of logarithmic functions are mainly based on the chain rule. However, we can generalize it for any differentiable function with. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend.
Introduction to Logarithmic Differentiation YouTube
However, we can generalize it for any differentiable function with. Derivatives of logarithmic functions are mainly based on the chain rule. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend.
Using Logs to help differentiate
However, we can generalize it for any differentiable function with. Derivatives of logarithmic functions are mainly based on the chain rule. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend.
core pure 3 notes differentiating natural logarithms and exponentials
However, we can generalize it for any differentiable function with. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend. Derivatives of logarithmic functions are mainly based on the chain rule.
Differentiating with Logs EX1 YouTube
However, we can generalize it for any differentiable function with. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend. Derivatives of logarithmic functions are mainly based on the chain rule.
Exponential Functions And Logs
However, we can generalize it for any differentiable function with. Derivatives of logarithmic functions are mainly based on the chain rule. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend.
Differentiating Natural log Functions 2 YouTube
However, we can generalize it for any differentiable function with. Derivatives of logarithmic functions are mainly based on the chain rule. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend.
12 x1 t01 02 differentiating logs (2013) PPT
However, we can generalize it for any differentiable function with. Derivatives of logarithmic functions are mainly based on the chain rule. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend.
However, We Can Generalize It For Any Differentiable Function With.
Derivatives of logarithmic functions are mainly based on the chain rule. We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(log_bx=\frac{\ln x}{\ln b}\) allows us to extend.