Differentiating A Matrix - It will always work to. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Review of multivariate differentiation, integration, and optimization, with applications to data science. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by.
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. It will always work to. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? Review of multivariate differentiation, integration, and optimization, with applications to data science.
If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. Review of multivariate differentiation, integration, and optimization, with applications to data science. It will always work to.
python Error implementing differentiating matrix using numpy Stack
Review of multivariate differentiation, integration, and optimization, with applications to data science. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. The derivative of a matrix \( a(t) \), whose elements depend.
calculus and analysis Differentiating matrix function in `Table` from
Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. It will always work to. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? If.
calculus and analysis Differentiating matrix function in `Table` from
It will always work to. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. Review of multivariate differentiation,.
Established Models Matrix
It will always work to. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a.
calculus Differentiating the matrix square root Mathematics Stack
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases what are some conventions for.
Established Models Matrix
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. It will always work to. Review of multivariate differentiation, integration, and optimization, with applications to data science. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? If.
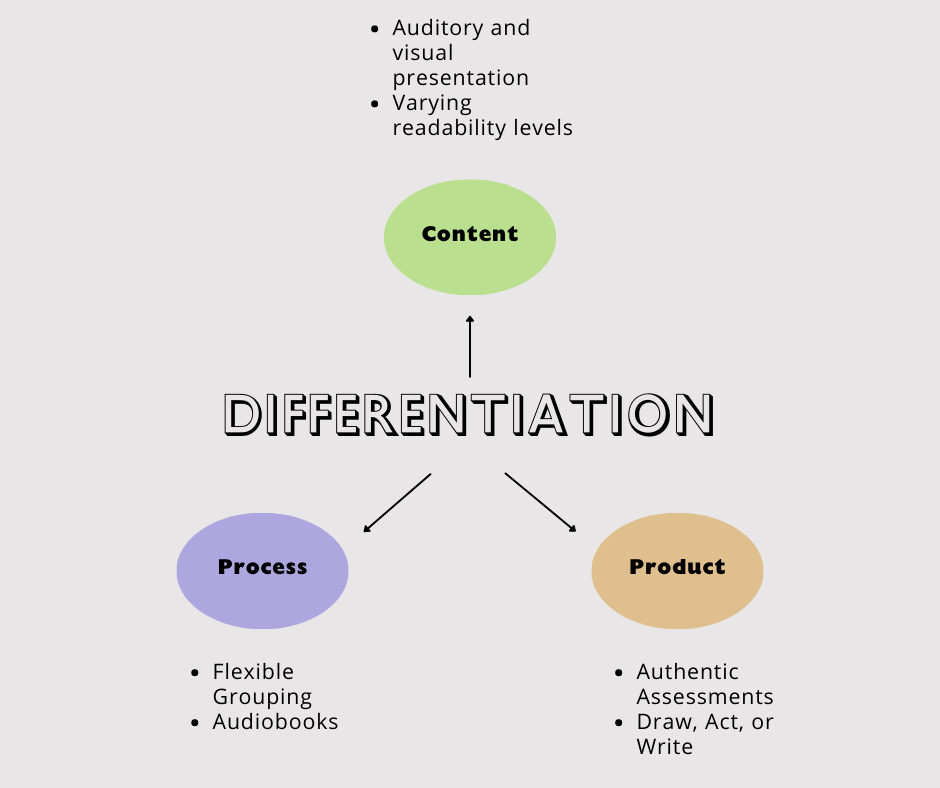
3 Ideas for Differentiating Instruction in Your Next Lesson Educator
If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Review of multivariate differentiation, integration, and optimization, with applications to data science. It will always work to. The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a.
3 Ways You Can Start Differentiating Math Today Teaching with Amanda
If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? It will always work to. Review of multivariate differentiation, integration, and optimization, with applications to data science. The derivative of a matrix \(.
Jumpstart Differentiating Assessments and Student Products in 3 Easy
Review of multivariate differentiation, integration, and optimization, with applications to data science. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? It will always work to. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. The derivative of a matrix \(.
python Error implementing differentiating matrix using numpy Stack
Review of multivariate differentiation, integration, and optimization, with applications to data science. It will always work to. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column. Matrix derivative common cases what are some conventions for derivatives of matrices and vectors? The derivative of a matrix \(.
Matrix Derivative Common Cases What Are Some Conventions For Derivatives Of Matrices And Vectors?
The derivative of a matrix \( a(t) \), whose elements depend on a scalar variable \( t \), is a new matrix where each element is obtained by. It will always work to. Review of multivariate differentiation, integration, and optimization, with applications to data science. If $m$ is your matrix, then it represents a linear $f\colon \mathbb{r}^n \to \mathbb{r}^n$, thus when you do $m(t)$ by row times column.