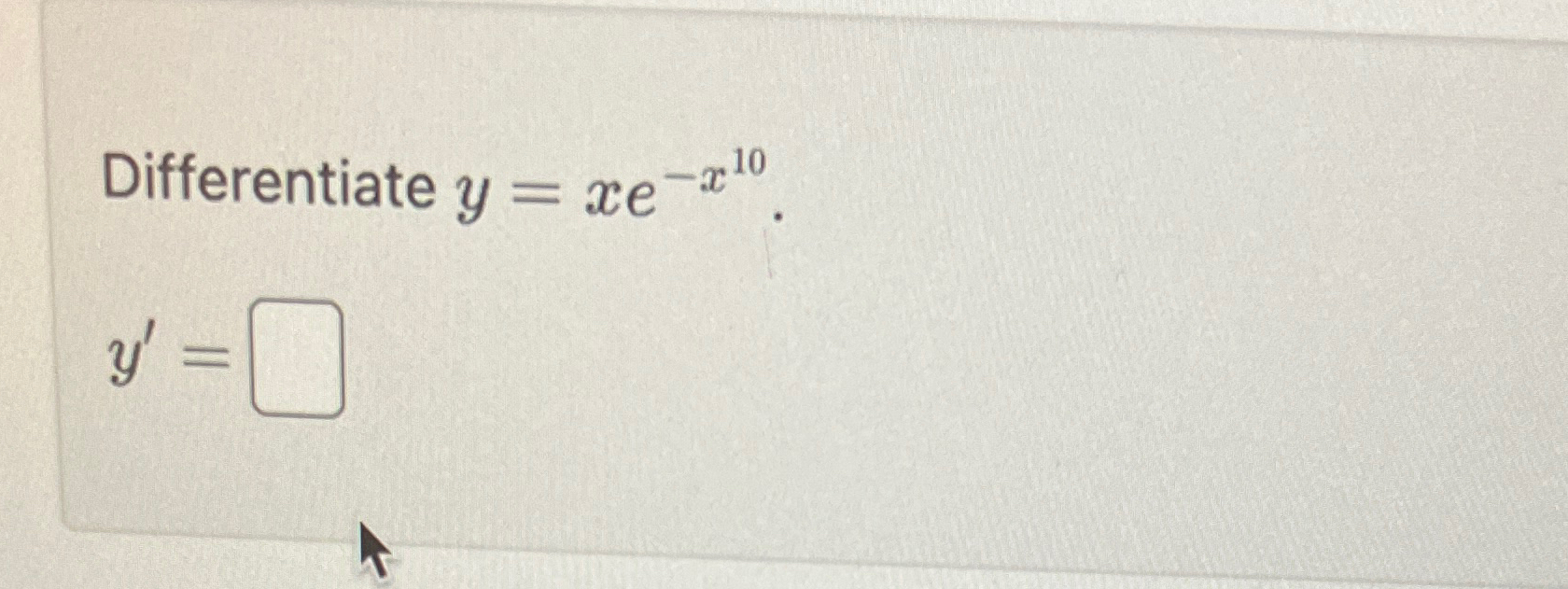Differentiate Xe X 2 - Find the derivative of f (x) = xlnx at the point x = e2. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = ex f (x) = e x and g(x). How to differentiate xe^ (x^2) in calculus, we have a special rule that we use when we want to find the derivative of a product of functions. The gradient is a vector with as many coordinates. Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x).
Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). The gradient is a vector with as many coordinates. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Find the derivative of f (x) = xlnx at the point x = e2. How to differentiate xe^ (x^2) in calculus, we have a special rule that we use when we want to find the derivative of a product of functions. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = ex f (x) = e x and g(x). Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x).
The gradient is a vector with as many coordinates. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = ex f (x) = e x and g(x). Find the derivative of f (x) = xlnx at the point x = e2. How to differentiate xe^ (x^2) in calculus, we have a special rule that we use when we want to find the derivative of a product of functions. Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x).
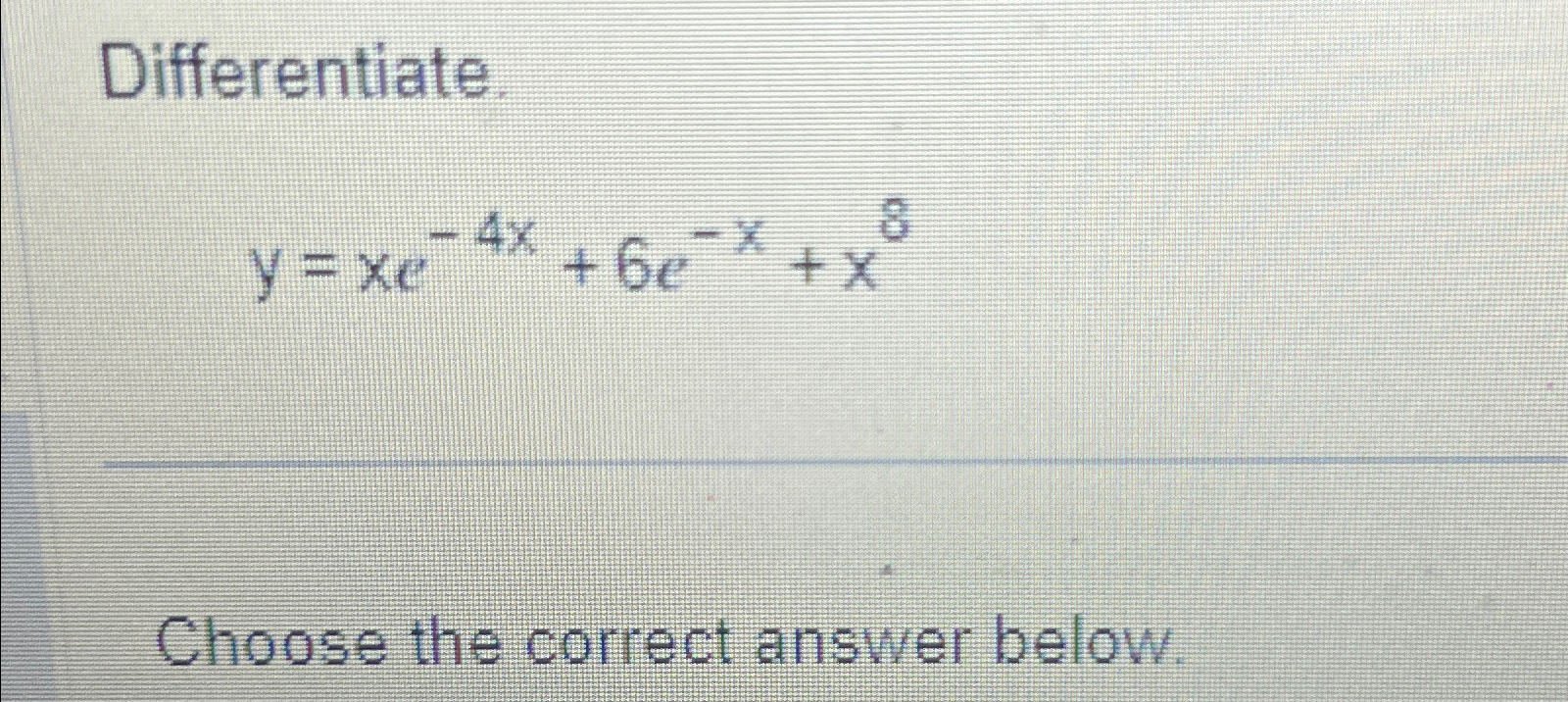
Solved Differentiate.y=xe4x+6ex+x8Choose the correct
The gradient is a vector with as many coordinates. Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Differentiate using the product rule.
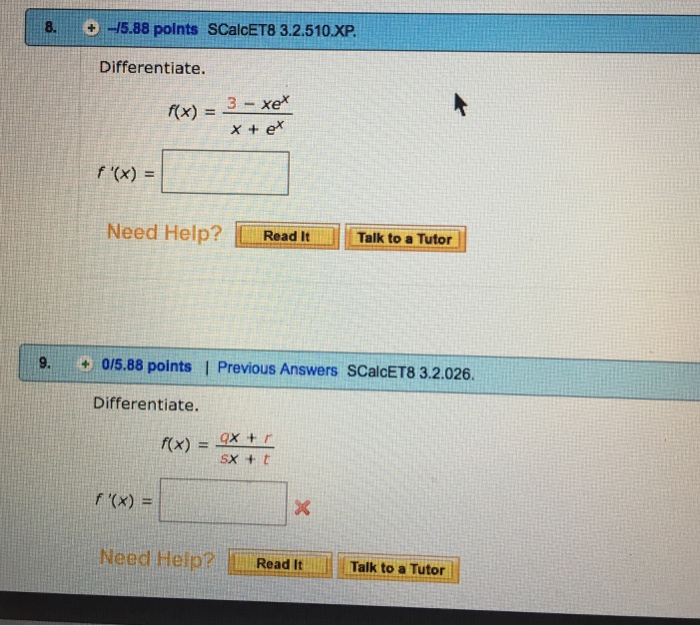
Solved Differentiate. F(x) = 3 xe^x/x + e^x f '(x) =
How to differentiate xe^ (x^2) in calculus, we have a special rule that we use when we want to find the derivative of a product of functions. Find the derivative of f (x) = xlnx at the point x = e2. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is.
Solved 16. Differentiate xe^(2x) with respect to x. [algebra]
Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). How to differentiate xe^ (x^2) in calculus, we have a special rule that we use when we want to find the derivative of.
Solved Differentiate the following. (a) y = xe^2x + e^x +
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = ex f (x) = e x and g(x). Find the derivative of f (x) = xlnx at the point x = e2. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge.
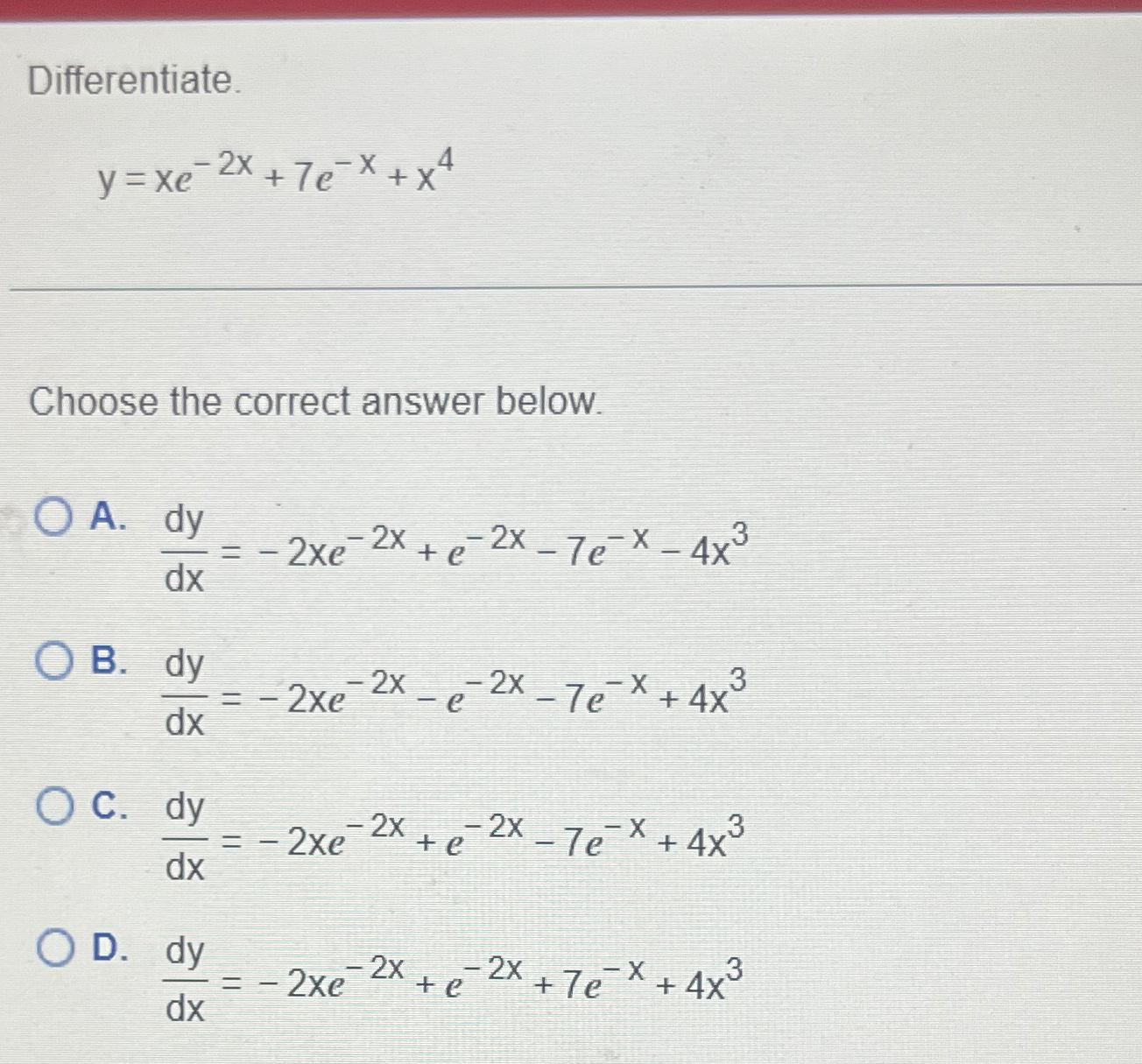
Solved Differentiate.y=xe2x+7ex+x4Choose the correct
Find the derivative of f (x) = xlnx at the point x = e2. Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). The gradient is a vector with as many coordinates..
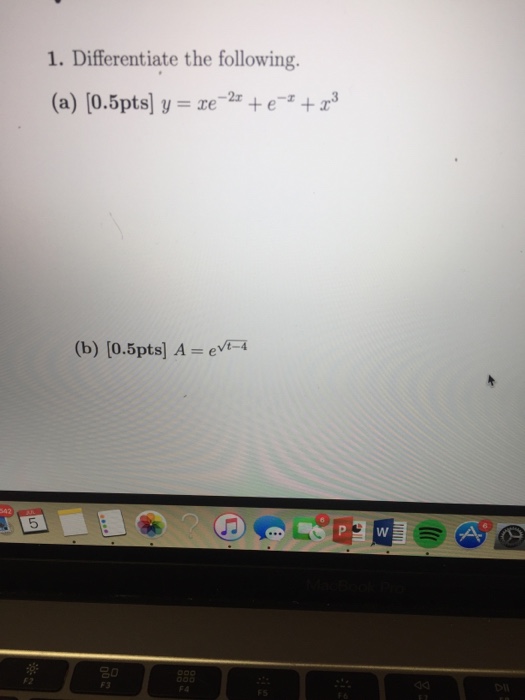
Solved 7. Differentiate Y=xe^2x+e^x+x^3 8. Find the
Find the derivative of f (x) = xlnx at the point x = e2. The gradient is a vector with as many coordinates. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = ex f (x) = e.
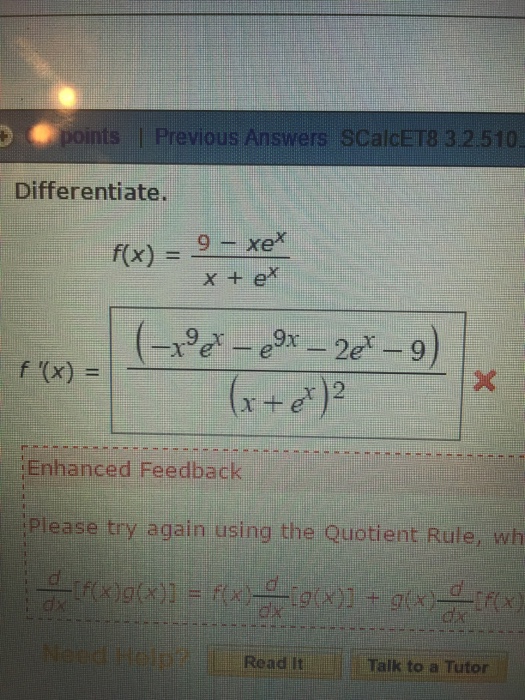
Solved Differentiate f(x)= (9xe^x)/(x+e^x)
How to differentiate xe^ (x^2) in calculus, we have a special rule that we use when we want to find the derivative of a product of functions. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = ex.
Solved Differentiate y=xex10.y'=
Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x).
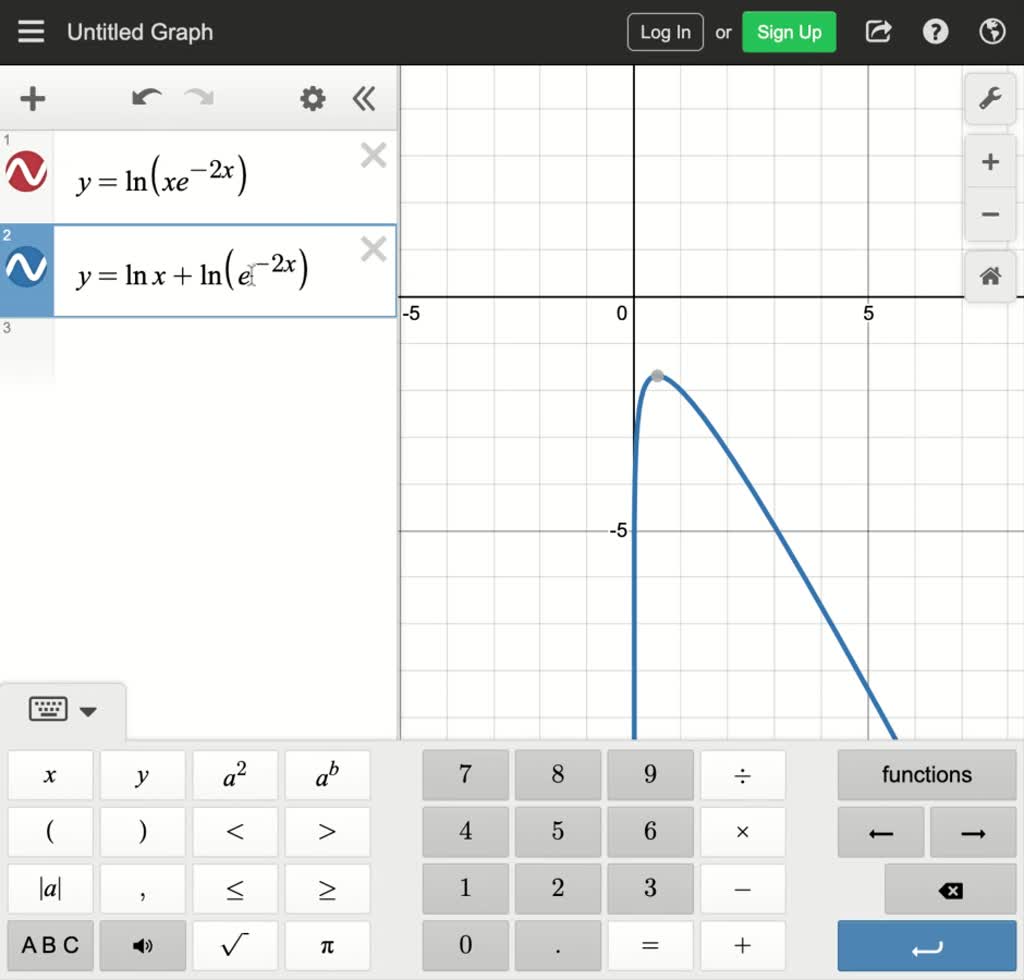
Differentiate the function. g(x) = ln(xe^2x) Numerade
Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). How to differentiate xe^ (x^2) in calculus, we have a special rule that we use when we want to find the derivative of.
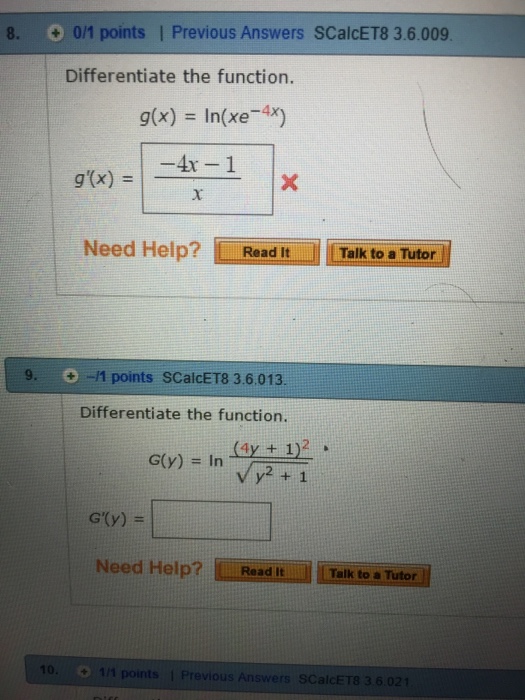
Solved Differentiate the function.g(x) =ln(xe^4x)g'(x) =
Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). How to differentiate xe^ (x^2) in calculus, we have a special rule that we use when we want to find the derivative of.
How To Differentiate Xe^ (X^2) In Calculus, We Have A Special Rule That We Use When We Want To Find The Derivative Of A Product Of Functions.
Find the derivative of f (x) = xlnx at the point x = e2. Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x). X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: Differentiate using the product rule which states that d dx[f (x)g(x)] d d x [f (x) g (x)] is f (x) d dx[g(x)]+g(x) d dx [f (x)] f (x) d d x [g (x)] + g (x).
Differentiate Using The Chain Rule, Which States That D Dx [F (G(X))] D D X [F (G (X))] Is F '(G(X))G'(X) F ′ (G (X)) G ′ (X) Where F (X) = Ex F (X) = E X And G(X).
The gradient is a vector with as many coordinates.