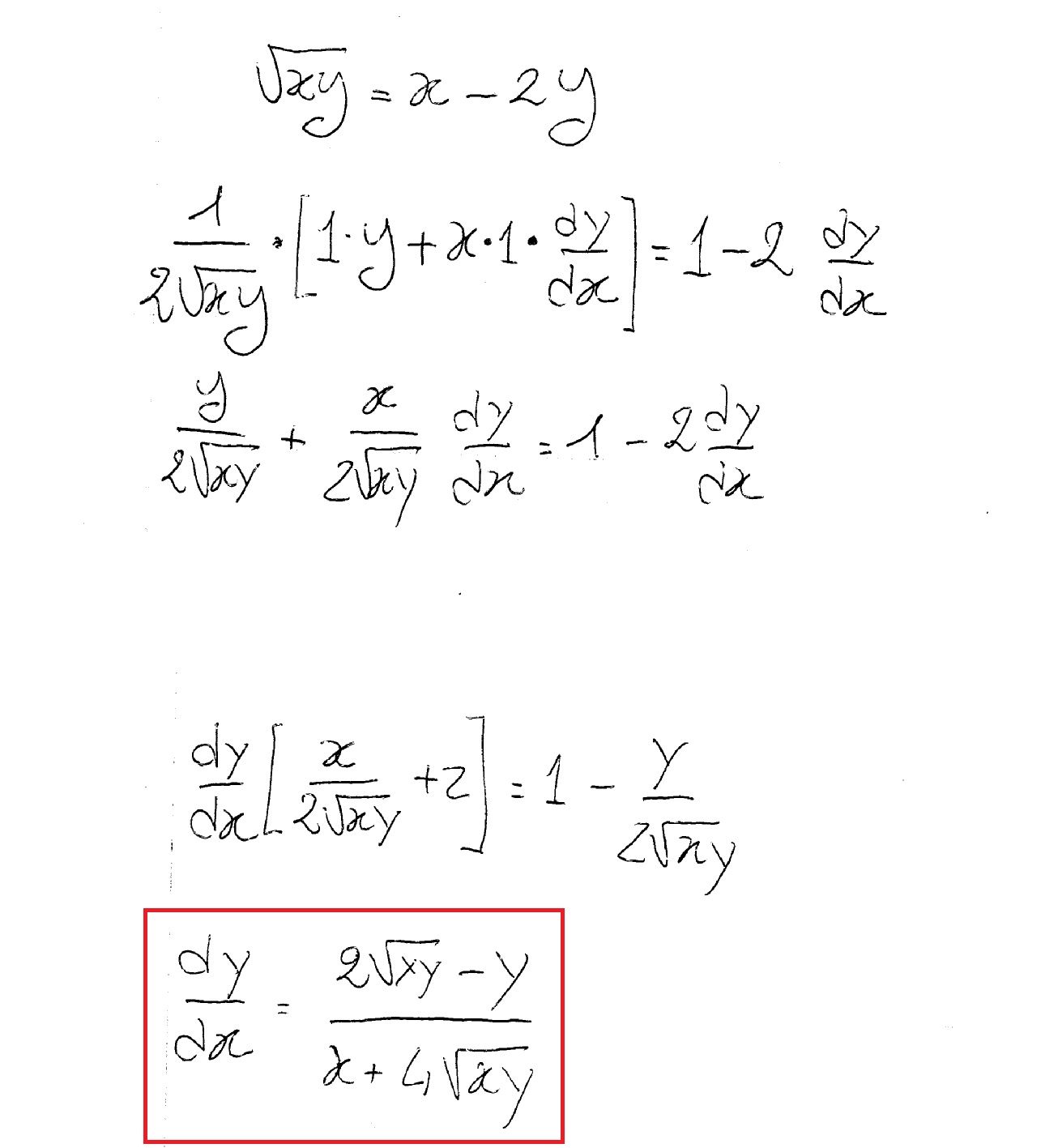Differentiate Sqrt X - This key question has an answer here:. If y = x n, then y ′ = n x n − 1. Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. Remember that we can rewrite surds like this in index notation. How do you find the derivative of y = √x using the definition of derivative? What is the derivative of square root of x? X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule. The derivative of \sqrt{x} can also be found using first principles. We rewrite root x using the rule of indices.
Remember that we can rewrite surds like this in index notation. $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule. What is the derivative of square root of x? This key question has an answer here:. The derivative of sqrt(x) is 1/(2sqrt(x)). The derivative of \sqrt{x} can also be found using first principles. Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: If y = x n, then y ′ = n x n − 1. We rewrite root x using the rule of indices.
Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. This key question has an answer here:. We rewrite root x using the rule of indices. X = x 1 2; If y = x n, then y ′ = n x n − 1. The derivative of sqrt(x) is 1/(2sqrt(x)). The derivative of \sqrt{x} can also be found using first principles. $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule. Remember that we can rewrite surds like this in index notation. Apply the above power rule.
3 Ways to Differentiate the Square Root of X wikiHow
What is the derivative of square root of x? Remember that we can rewrite surds like this in index notation. X = x 1 2; X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule.
How do you differentiate 5/x^2? Socratic
We rewrite root x using the rule of indices. What is the derivative of square root of x? X = x 1 2; The derivative of \sqrt{x} can also be found using first principles. $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule.
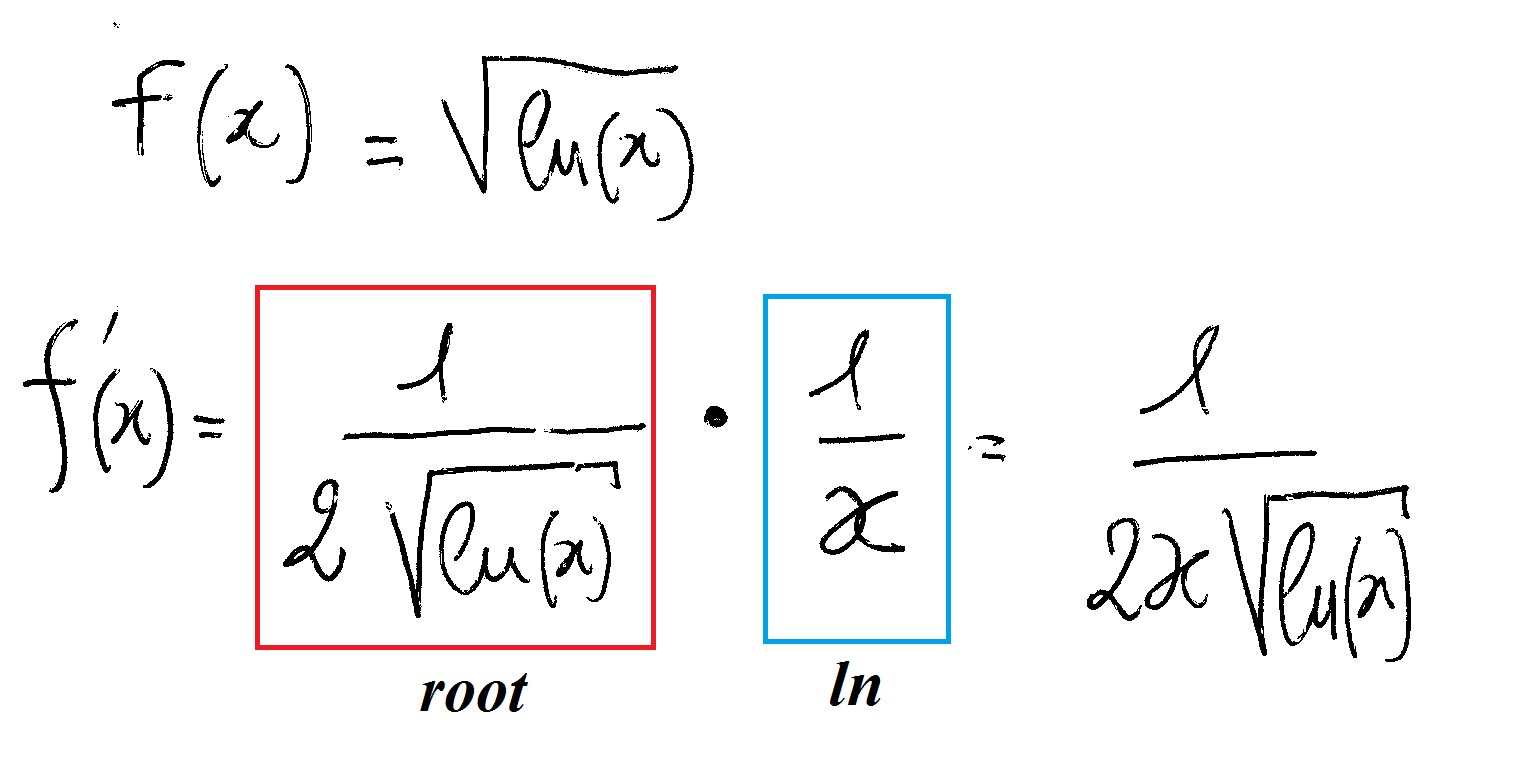
What is the derivative of the sqrt ln x? Socratic
How do you find the derivative of y = √x using the definition of derivative? What is the derivative of square root of x? We rewrite root x using the rule of indices. Apply the above power rule. Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and.
3 Ways to Differentiate the Square Root of X wikiHow
If y = x n, then y ′ = n x n − 1. Apply the above power rule. How do you find the derivative of y = √x using the definition of derivative? We rewrite root x using the rule of indices. Remember that we can rewrite surds like this in index notation.
3 Ways to Differentiate the Square Root of X wikiHow
What is the derivative of square root of x? Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. Remember that we can rewrite surds like this in index notation. The derivative of sqrt(x) is 1/(2sqrt(x)). How do you find the derivative of y = √x using the definition of derivative?
How do you differentiate sqrt(xy) = x 2y? Socratic
X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: If y = x n, then y ′ = n x n − 1. The derivative of \sqrt{x} can also be found using first principles. X = x 1 2; This key question has an answer here:.
trigonometry About proof \cot^{1}\left(\frac{\sqrt{1+\sin x}+\sqrt
$$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: If y = x n, then y ′ = n x n − 1. The derivative of sqrt(x) is 1/(2sqrt(x)). We rewrite root x using the rule of indices.
Solved Answer Preview Result [sqrt(x+1) (x1)I(x+1)(x1)1)
If y = x n, then y ′ = n x n − 1. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: The derivative of sqrt(x) is 1/(2sqrt(x)). This key question has an answer here:. We rewrite root x using the rule of indices.
calculus Differentiate y = x^{\sqrt{x}} (Simplification
How do you find the derivative of y = √x using the definition of derivative? The derivative of sqrt(x) is 1/(2sqrt(x)). What is the derivative of square root of x? $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule. X = x 1 2;
How do you differentiate y = arccosx + x sqrt(1x^2)? Socratic
If y = x n, then y ′ = n x n − 1. What is the derivative of square root of x? Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. The derivative of sqrt(x) is 1/(2sqrt(x)). Apply the above power rule.
What Is The Derivative Of Square Root Of X?
How do you find the derivative of y = √x using the definition of derivative? Remember that we can rewrite surds like this in index notation. If y = x n, then y ′ = n x n − 1. This key question has an answer here:.
The Derivative Of Sqrt(X) Is 1/(2Sqrt(X)).
Apply the above power rule. Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: X = x 1 2;
The Derivative Of \Sqrt{X} Can Also Be Found Using First Principles.
We rewrite root x using the rule of indices. $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule.