Differentiality - If the left hand derivative and the right hand derivative at a point are equal. Some places define it as: Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: The theorems assure us that essentially all functions that we see in the course.
If the left hand derivative and the right hand derivative at a point are equal. The theorems assure us that essentially all functions that we see in the course. Some places define it as: Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions:
Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: If the left hand derivative and the right hand derivative at a point are equal. The theorems assure us that essentially all functions that we see in the course. Some places define it as:
13 4 Calculate the Total Differential YouTube
Some places define it as: The theorems assure us that essentially all functions that we see in the course. If the left hand derivative and the right hand derivative at a point are equal. Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions:
Differentials YouTube
Some places define it as: The theorems assure us that essentially all functions that we see in the course. If the left hand derivative and the right hand derivative at a point are equal. Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions:
Using Differentials YouTube
Some places define it as: Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: The theorems assure us that essentially all functions that we see in the course. If the left hand derivative and the right hand derivative at a point are equal.
Pin on School Stuff
Some places define it as: The theorems assure us that essentially all functions that we see in the course. If the left hand derivative and the right hand derivative at a point are equal. Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions:
Total Differential Problems & Solutions Part 2 YouTube
If the left hand derivative and the right hand derivative at a point are equal. Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: Some places define it as: The theorems assure us that essentially all functions that we see in the course.
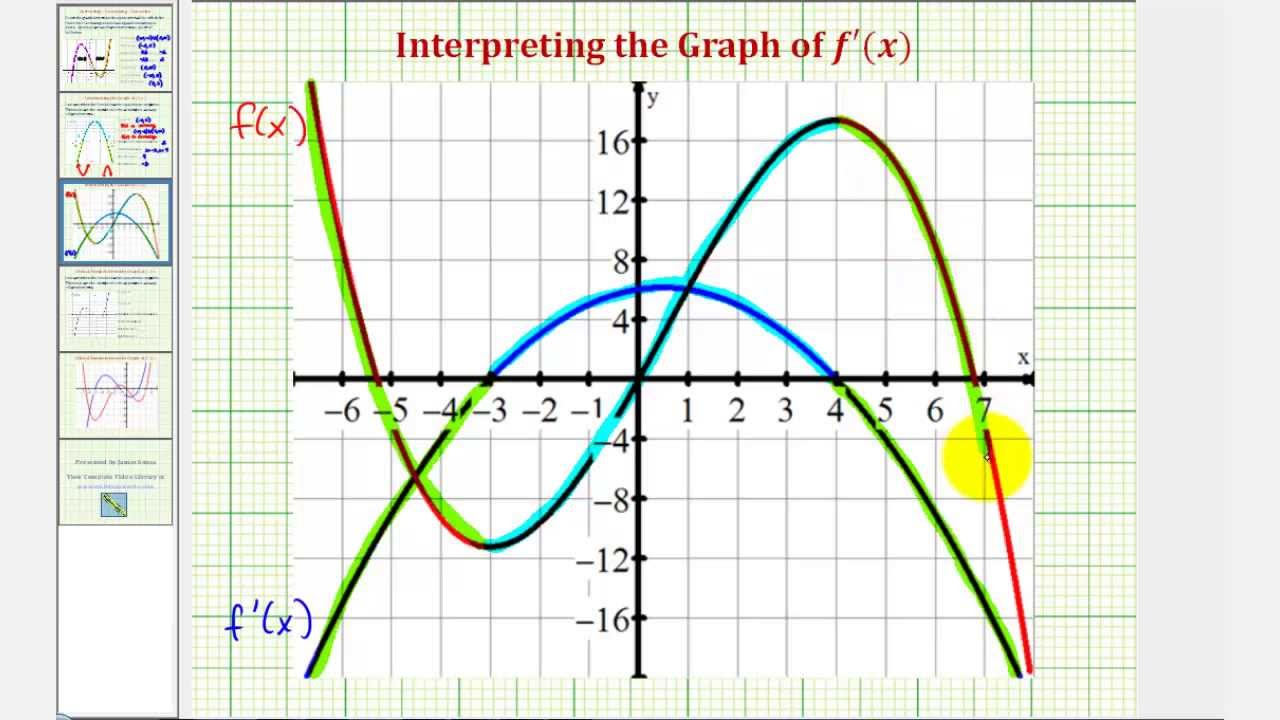
Ex 1 Interpret the Graph of the First Derivative Function Degree 2
If the left hand derivative and the right hand derivative at a point are equal. The theorems assure us that essentially all functions that we see in the course. Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: Some places define it as:
Continuity and Differentiability YouTube
If the left hand derivative and the right hand derivative at a point are equal. Some places define it as: Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: The theorems assure us that essentially all functions that we see in the course.
Ex 1 Determine Differential y (dy) YouTube
If the left hand derivative and the right hand derivative at a point are equal. The theorems assure us that essentially all functions that we see in the course. Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: Some places define it as:
Chapter 1 Differential YouTube
If the left hand derivative and the right hand derivative at a point are equal. Some places define it as: Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: The theorems assure us that essentially all functions that we see in the course.
![Testing Multivariate Normality using R [Bengali] YouTube](https://i.ytimg.com/vi/-2D2bcpNJpg/maxresdefault.jpg)
Testing Multivariate Normality using R [Bengali] YouTube
Some places define it as: Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: The theorems assure us that essentially all functions that we see in the course. If the left hand derivative and the right hand derivative at a point are equal.
The Theorems Assure Us That Essentially All Functions That We See In The Course.
Some places define it as: Lim x→a f(x) exists lim x→a f(x) = f(a) characteristics of continuous functions: If the left hand derivative and the right hand derivative at a point are equal.