Differential Equations Eigenvalues And Eigenvectors - So we will look for solutions y1 = e ta. The concept of eigenvalues and eigenvectors. In this section we will introduce the concept of eigenvalues and eigenvectors of a. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. This chapter ends by solving linear differential equations du/dt = au. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This short paper not only explains the connection between eigenvalues, eigenvectors and. We've seen that solutions to linear odes have the form ert. The pieces of the solution. Consider a linear homogeneous system of n.
This short paper not only explains the connection between eigenvalues, eigenvectors and. The concept of eigenvalues and eigenvectors. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. In this section we will introduce the concept of eigenvalues and eigenvectors of a. This chapter ends by solving linear differential equations du/dt = au. The pieces of the solution. So we will look for solutions y1 = e ta. We've seen that solutions to linear odes have the form ert. Consider a linear homogeneous system of n.
This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. The pieces of the solution. So we will look for solutions y1 = e ta. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. In this section we will introduce the concept of eigenvalues and eigenvectors of a. This short paper not only explains the connection between eigenvalues, eigenvectors and. This chapter ends by solving linear differential equations du/dt = au. Consider a linear homogeneous system of n. The concept of eigenvalues and eigenvectors. We've seen that solutions to linear odes have the form ert.
linear algebra Using eigenvectors and values to get systems of
So we will look for solutions y1 = e ta. The concept of eigenvalues and eigenvectors. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. In this section we will introduce the concept of eigenvalues and eigenvectors of a. We've seen that solutions to linear odes have the form ert.
How to Find Eigenvalues and Eigenvectors 8 Steps (with Pictures)
So we will look for solutions y1 = e ta. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. In this section we will introduce the concept of eigenvalues and eigenvectors of a. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This chapter ends by solving linear differential equations du/dt = au.
(PDF) Differential Equations Review _ Eigenvalues & Eigenvectors
The pieces of the solution. In this section we will introduce the concept of eigenvalues and eigenvectors of a. Consider a linear homogeneous system of n. We've seen that solutions to linear odes have the form ert. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
Solved Application of eigenvalues and eigenvectors to
In this section we will introduce the concept of eigenvalues and eigenvectors of a. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. Consider a linear homogeneous system of n. The pieces of the solution. We've seen that solutions to linear odes have the form ert.
How to Find Eigenvalues and Eigenvectors 8 Steps (with Pictures)
Consider a linear homogeneous system of n. In this section we will introduce the concept of eigenvalues and eigenvectors of a. This short paper not only explains the connection between eigenvalues, eigenvectors and. This chapter ends by solving linear differential equations du/dt = au. The concept of eigenvalues and eigenvectors.
(PDF) Linear Algebra Eigenvalues, Eigenvectors, and Differential
Understanding eigenvalues and eigenvectors is essential for solving systems of differential. Consider a linear homogeneous system of n. This short paper not only explains the connection between eigenvalues, eigenvectors and. We've seen that solutions to linear odes have the form ert. So we will look for solutions y1 = e ta.
Solved (a) Using eigenvalues and eigenvectors, solve the
The pieces of the solution. This chapter ends by solving linear differential equations du/dt = au. So we will look for solutions y1 = e ta. Consider a linear homogeneous system of n. This short paper not only explains the connection between eigenvalues, eigenvectors and.
Solved Solve the given system of differential equations
We've seen that solutions to linear odes have the form ert. Consider a linear homogeneous system of n. So we will look for solutions y1 = e ta. This chapter ends by solving linear differential equations du/dt = au. Understanding eigenvalues and eigenvectors is essential for solving systems of differential.
eigenvalues eigenvectors Differential Equations Direction Field
This chapter ends by solving linear differential equations du/dt = au. We've seen that solutions to linear odes have the form ert. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. The concept of eigenvalues and eigenvectors. This short paper not only explains the connection between eigenvalues, eigenvectors and.
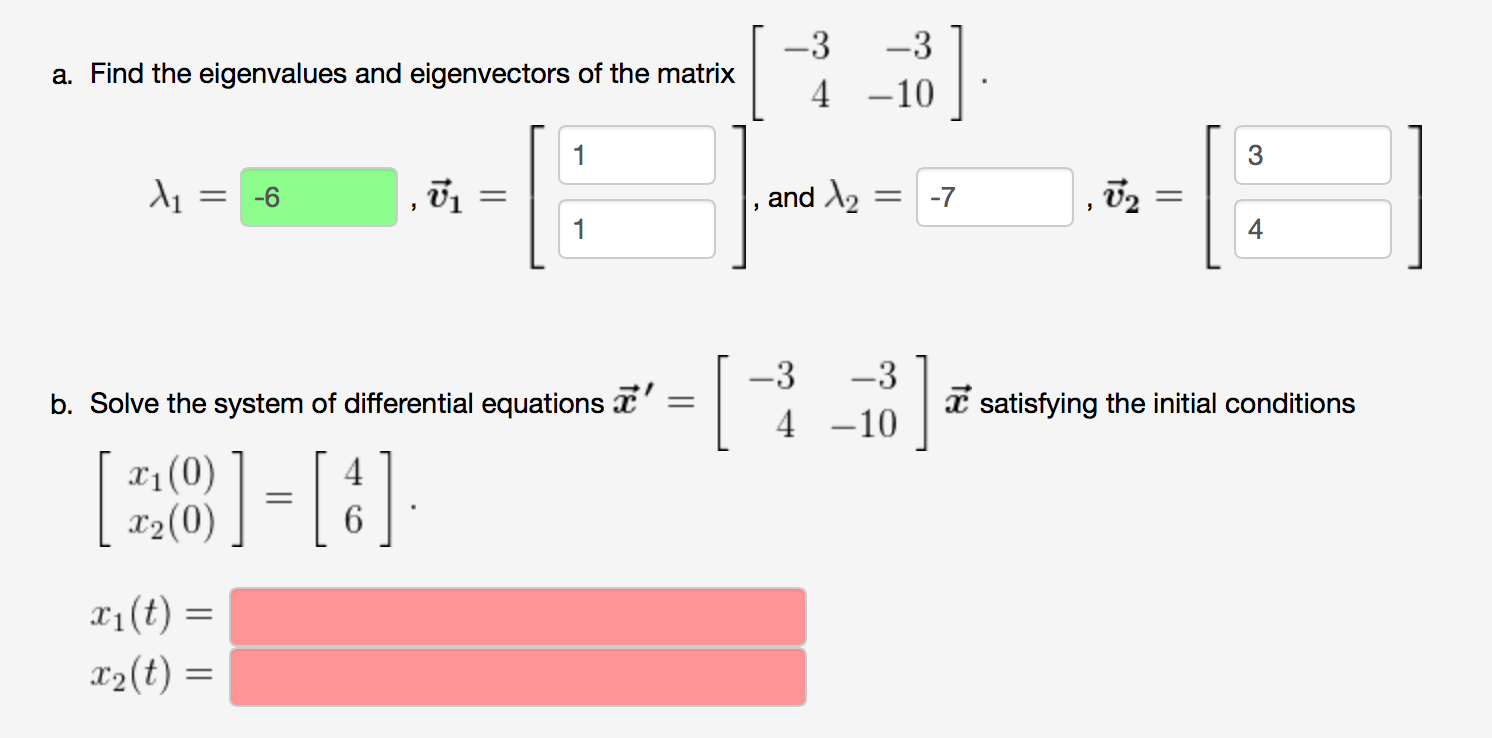
Solved a. Find the eigenvalues and eigenvectors of the
The pieces of the solution. The concept of eigenvalues and eigenvectors. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. Consider a linear homogeneous system of n. This short paper not only explains the connection between eigenvalues, eigenvectors and.
In This Section We Will Introduce The Concept Of Eigenvalues And Eigenvectors Of A.
The pieces of the solution. So we will look for solutions y1 = e ta. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. Consider a linear homogeneous system of n.
We've Seen That Solutions To Linear Odes Have The Form Ert.
The concept of eigenvalues and eigenvectors. This short paper not only explains the connection between eigenvalues, eigenvectors and. This chapter ends by solving linear differential equations du/dt = au. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.