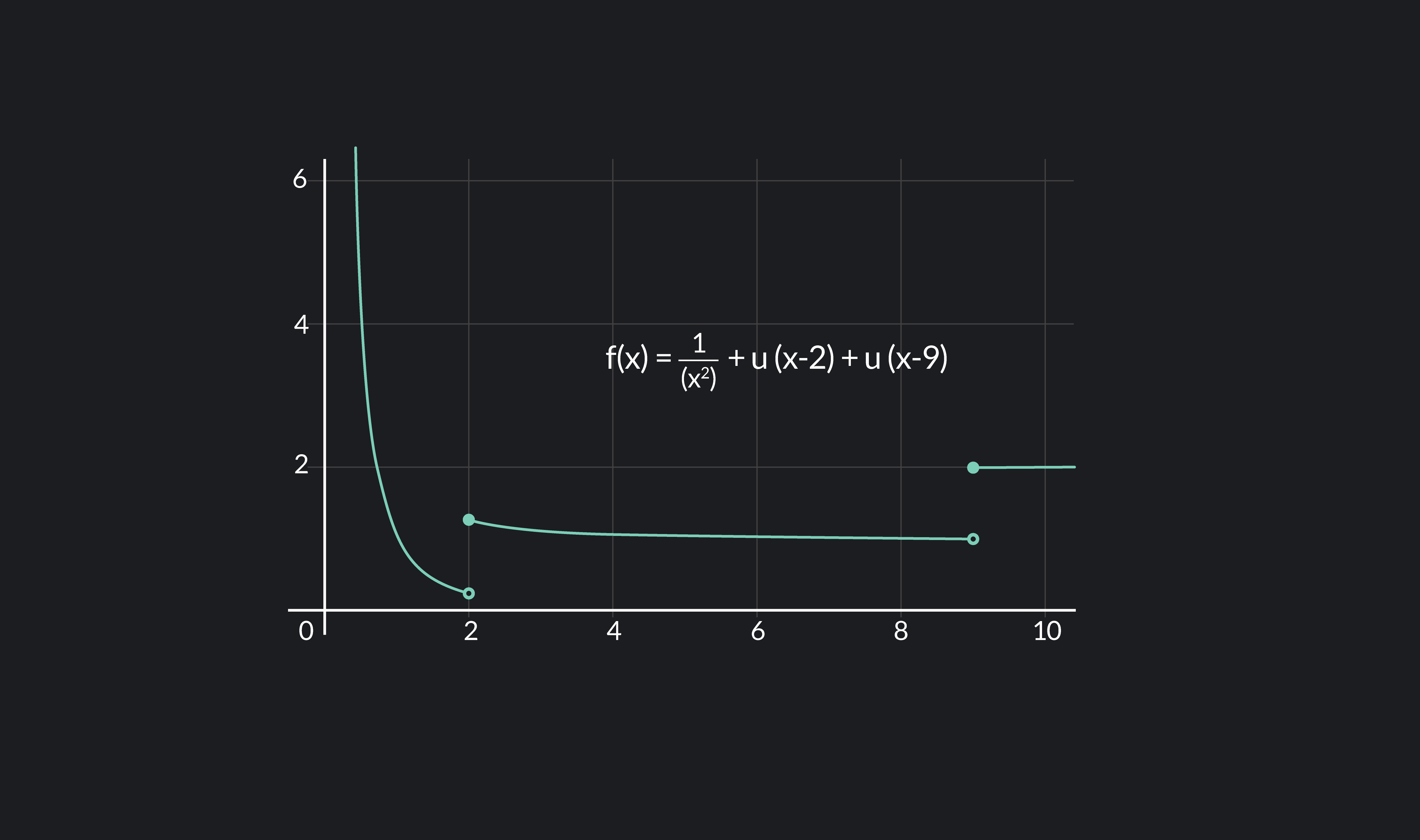
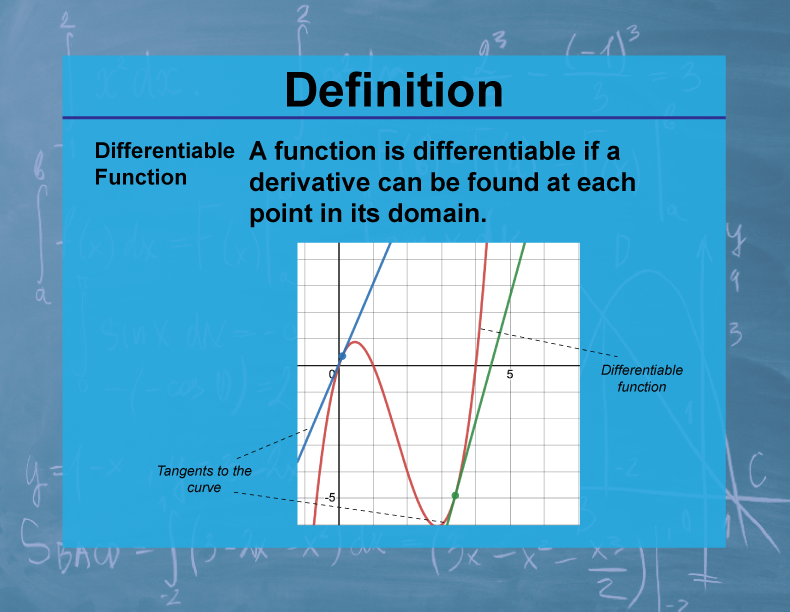
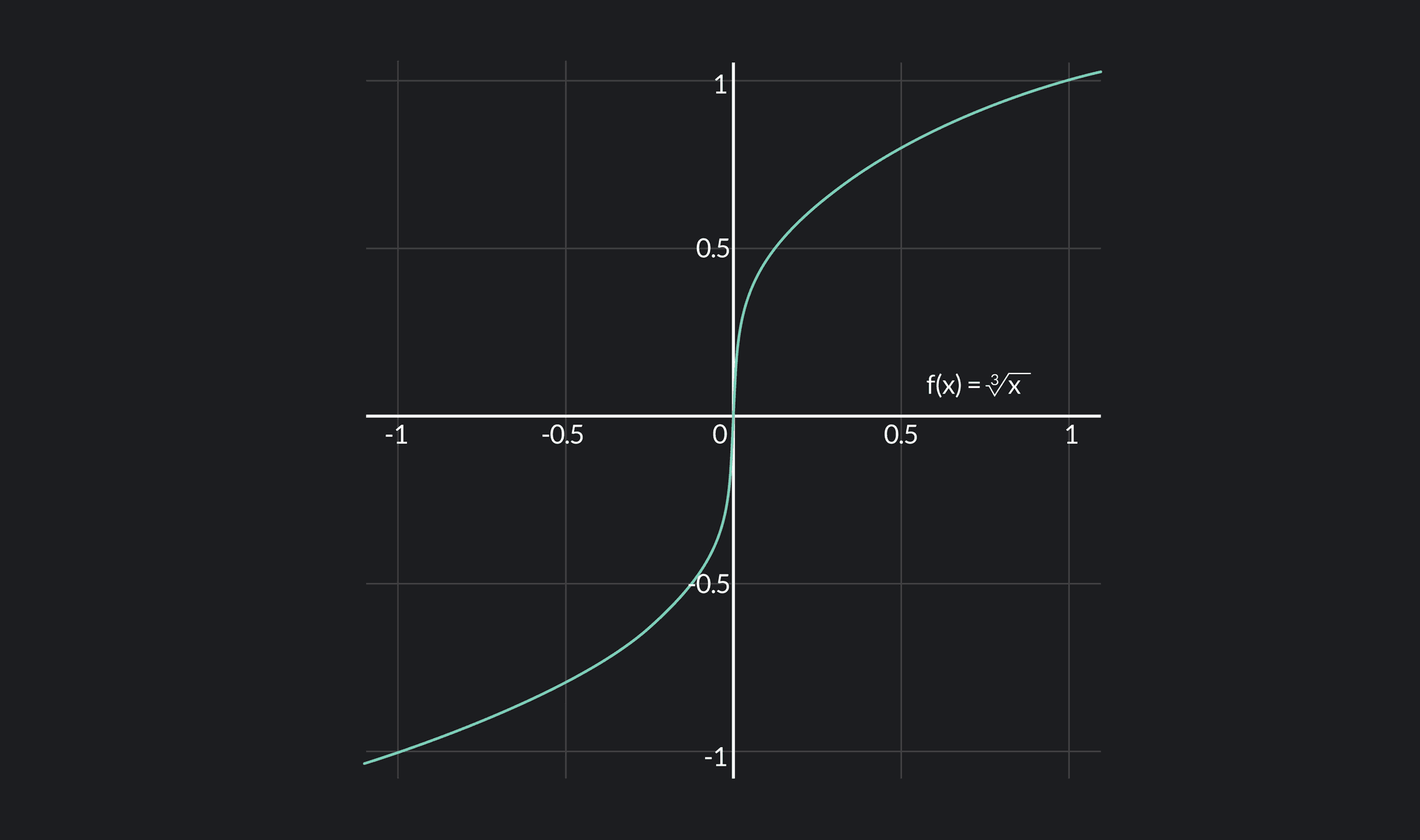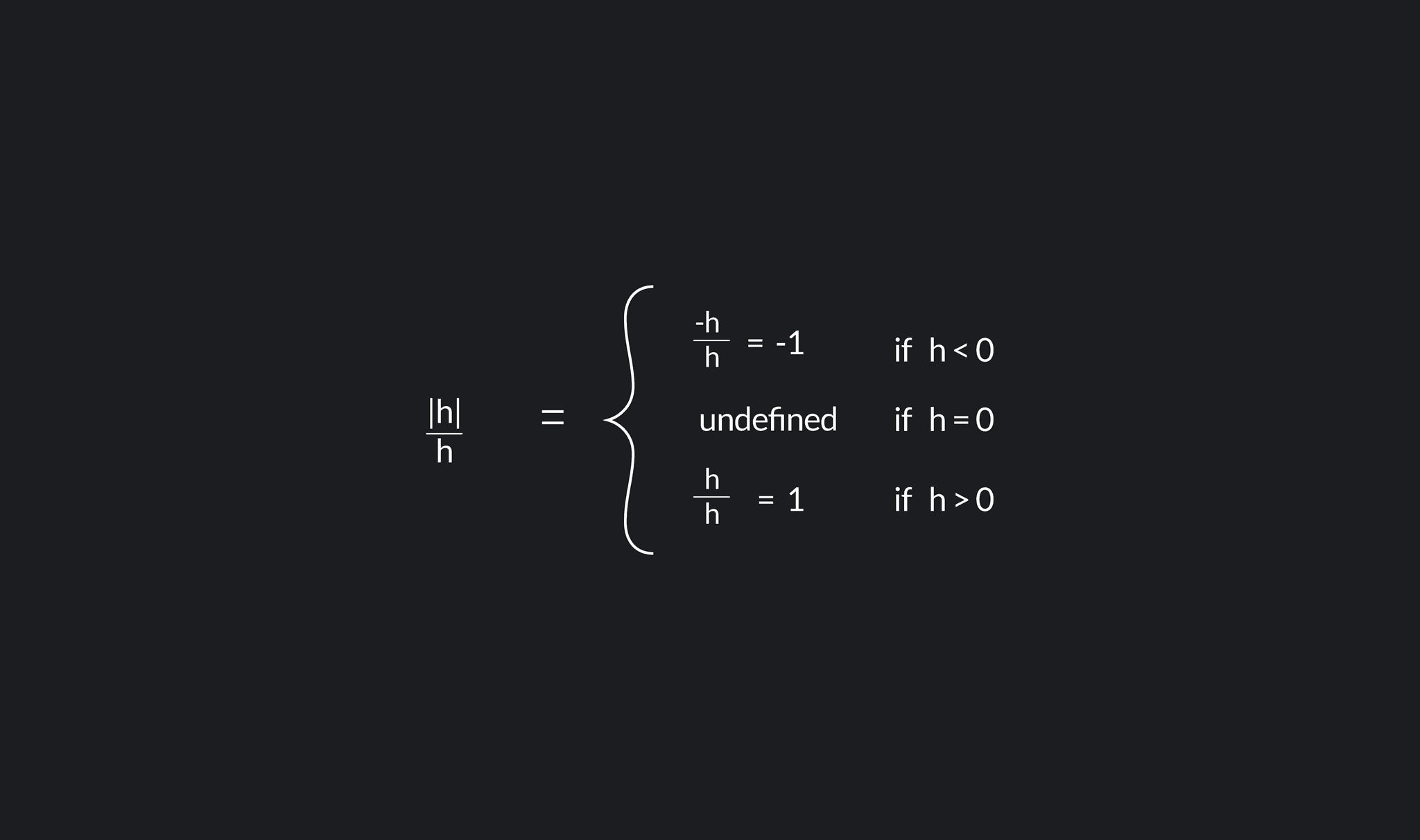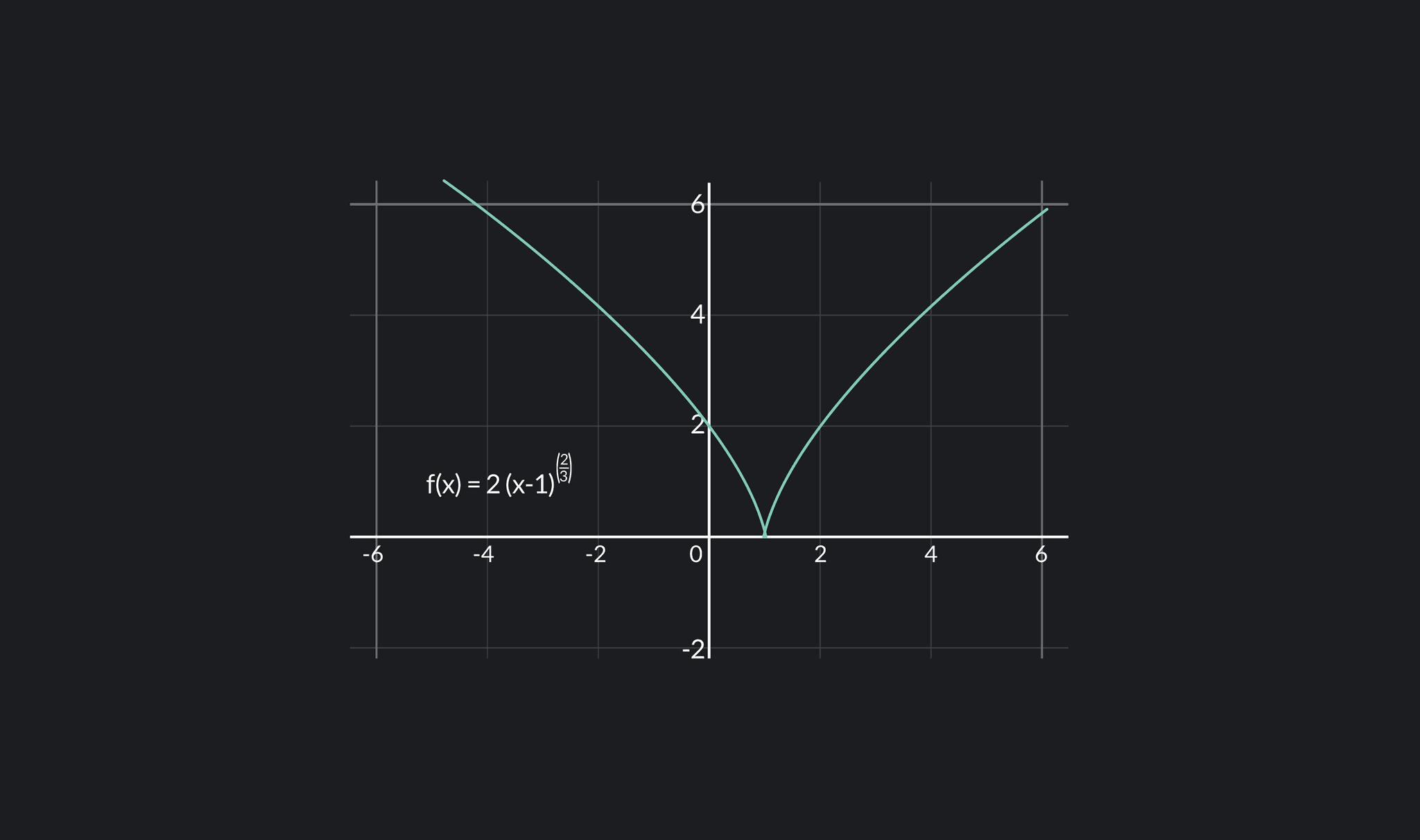Definition Of Differentiable - In calculus, a differentiable function is a continuous function whose derivative exists at all points on. This section has given us a formal definition of what it means for a functions to be. A function is differentiable (has a derivative) at point x if the following limit exists:
In calculus, a differentiable function is a continuous function whose derivative exists at all points on. This section has given us a formal definition of what it means for a functions to be. A function is differentiable (has a derivative) at point x if the following limit exists:
In calculus, a differentiable function is a continuous function whose derivative exists at all points on. A function is differentiable (has a derivative) at point x if the following limit exists: This section has given us a formal definition of what it means for a functions to be.
Differentiable Function Meaning, Formulas and Examples Outlier
In calculus, a differentiable function is a continuous function whose derivative exists at all points on. A function is differentiable (has a derivative) at point x if the following limit exists: This section has given us a formal definition of what it means for a functions to be.
Differentiable Function Meaning, Formulas and Examples Outlier
A function is differentiable (has a derivative) at point x if the following limit exists: In calculus, a differentiable function is a continuous function whose derivative exists at all points on. This section has given us a formal definition of what it means for a functions to be.
Differentiable vs. Continuous Functions Understanding the Distinctions
This section has given us a formal definition of what it means for a functions to be. In calculus, a differentiable function is a continuous function whose derivative exists at all points on. A function is differentiable (has a derivative) at point x if the following limit exists:
Differentiable function Wikiwand
In calculus, a differentiable function is a continuous function whose derivative exists at all points on. A function is differentiable (has a derivative) at point x if the following limit exists: This section has given us a formal definition of what it means for a functions to be.
Differentiable Font download free
This section has given us a formal definition of what it means for a functions to be. In calculus, a differentiable function is a continuous function whose derivative exists at all points on. A function is differentiable (has a derivative) at point x if the following limit exists:
Differentiable Function Meaning, Formulas and Examples Outlier
A function is differentiable (has a derivative) at point x if the following limit exists: This section has given us a formal definition of what it means for a functions to be. In calculus, a differentiable function is a continuous function whose derivative exists at all points on.
Differentiable Function Meaning, Formulas and Examples Outlier
A function is differentiable (has a derivative) at point x if the following limit exists: In calculus, a differentiable function is a continuous function whose derivative exists at all points on. This section has given us a formal definition of what it means for a functions to be.
DefinitionCalculus TopicsDifferentiable Function Media4Math
In calculus, a differentiable function is a continuous function whose derivative exists at all points on. A function is differentiable (has a derivative) at point x if the following limit exists: This section has given us a formal definition of what it means for a functions to be.
Differentiable Cuemath
In calculus, a differentiable function is a continuous function whose derivative exists at all points on. This section has given us a formal definition of what it means for a functions to be. A function is differentiable (has a derivative) at point x if the following limit exists:
Differentiable Cuemath
A function is differentiable (has a derivative) at point x if the following limit exists: In calculus, a differentiable function is a continuous function whose derivative exists at all points on. This section has given us a formal definition of what it means for a functions to be.
In Calculus, A Differentiable Function Is A Continuous Function Whose Derivative Exists At All Points On.
This section has given us a formal definition of what it means for a functions to be. A function is differentiable (has a derivative) at point x if the following limit exists: