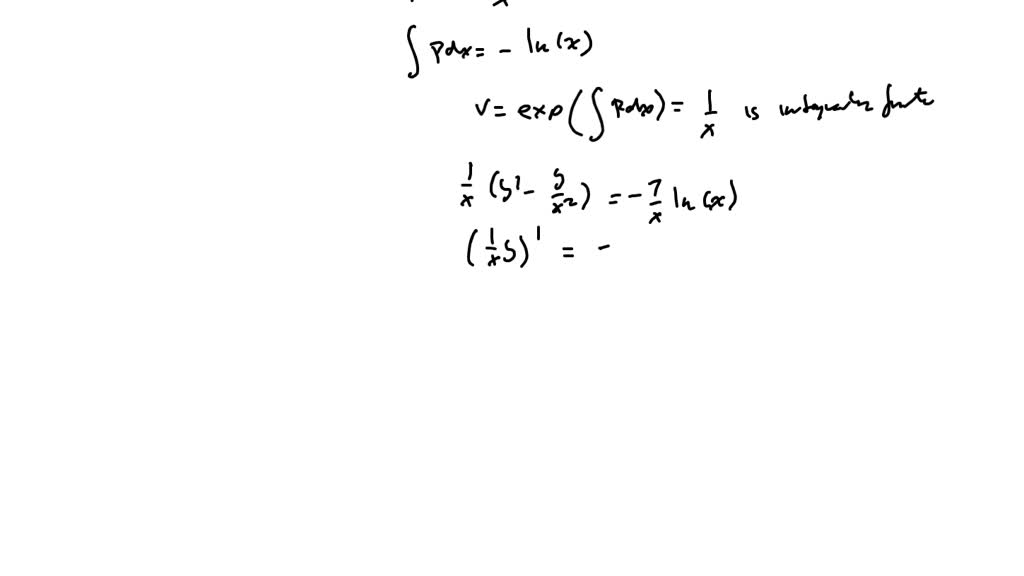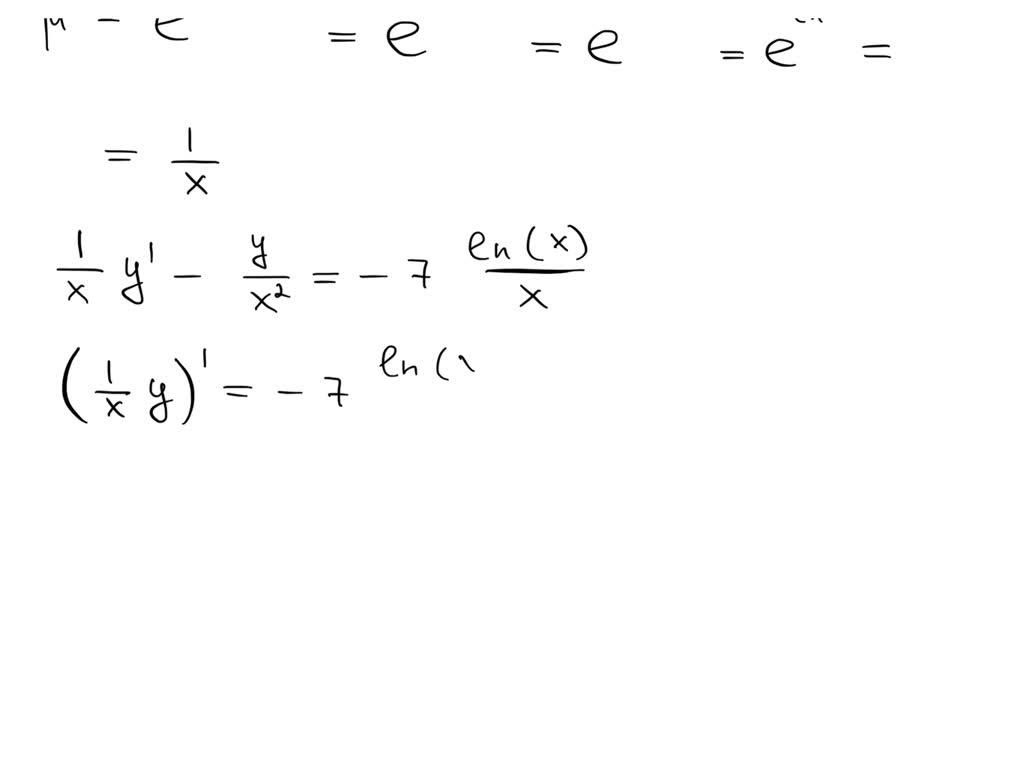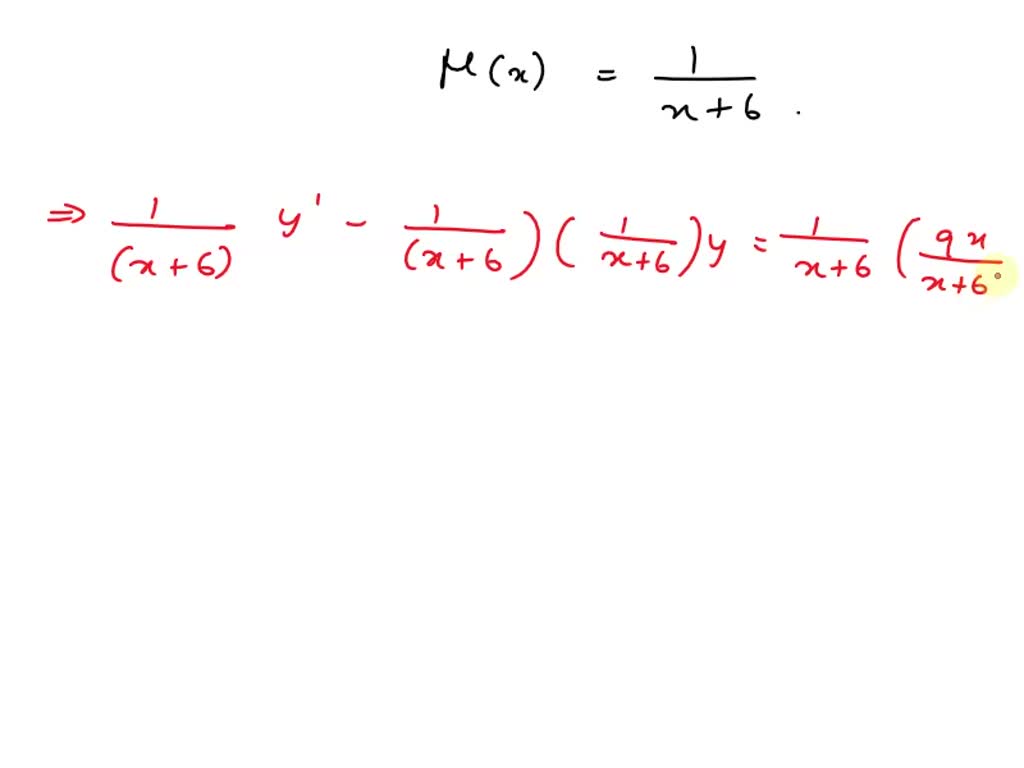Solve The Following Differential Equation By Using Integrating Factors. - Can be solved using the integrating factor method. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e. After writing the equation in standard form, p(x) can be.
A linear first order o.d.e. Can be solved using the integrating factor method. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. After writing the equation in standard form, p(x) can be.
Can be solved using the integrating factor method. A linear first order o.d.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. After writing the equation in standard form, p(x) can be.
Solved Which of the following is the appropriate integrating
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Can be solved using the integrating factor method. After writing the equation in standard form, p(x) can be. A linear first order o.d.e.
VIDEO solution Solve the differential equation y by using integrating
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e. After writing the equation in standard form, p(x) can be. Can be solved using the integrating factor method.
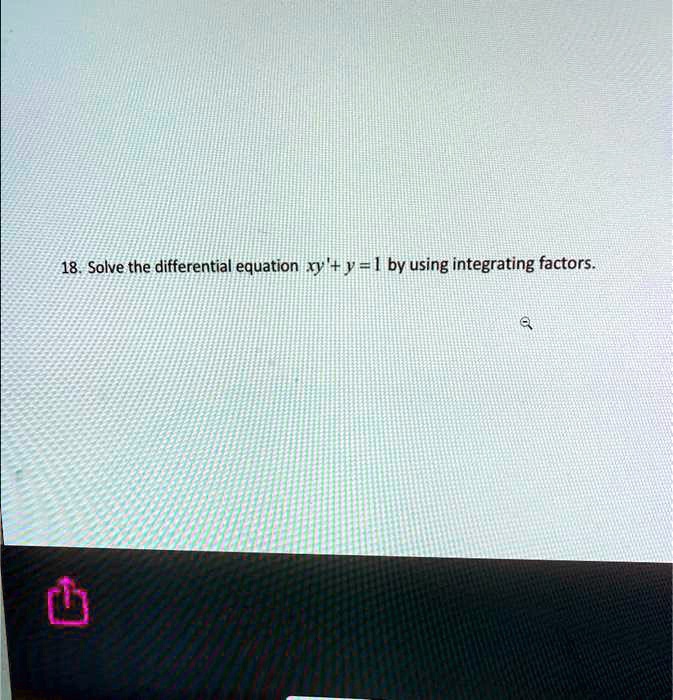
SOLVED Solve the following differential equation by using integrating
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. After writing the equation in standard form, p(x) can be. A linear first order o.d.e. Can be solved using the integrating factor method.
integrating factor of the differential equation X dy/dxy = 2 x ^2 is A
A linear first order o.d.e. Can be solved using the integrating factor method. After writing the equation in standard form, p(x) can be. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
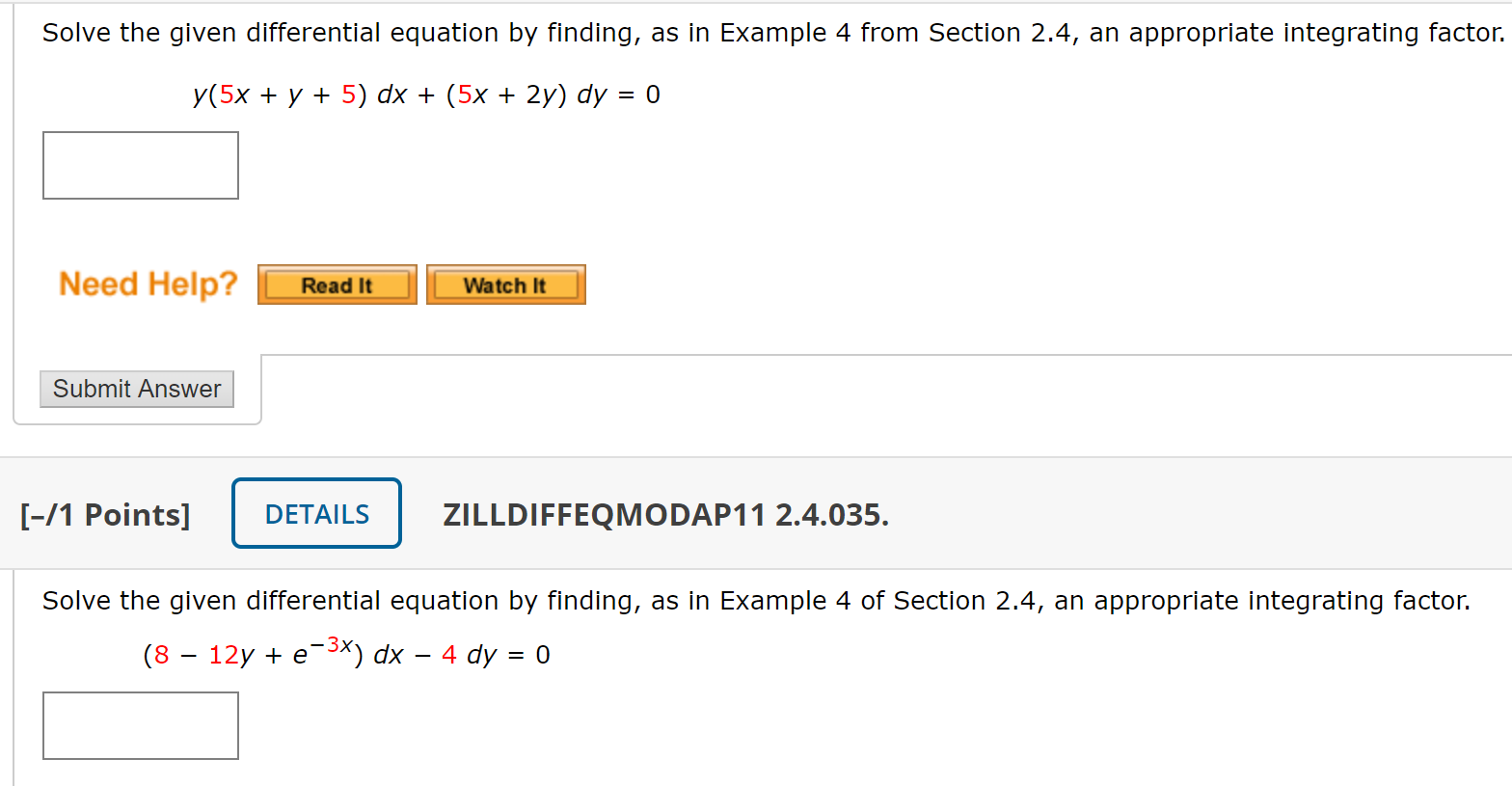
Solved Solve the given differential equation by finding, as
Can be solved using the integrating factor method. A linear first order o.d.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. After writing the equation in standard form, p(x) can be.
SOLVED Solve the following differential equation by using integrating
Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e. After writing the equation in standard form, p(x) can be. Can be solved using the integrating factor method.
Solved By finding an appropriate integrating factor, solve
After writing the equation in standard form, p(x) can be. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Can be solved using the integrating factor method. A linear first order o.d.e.
VIDEO solution Solve the following differential equation by using
Can be solved using the integrating factor method. After writing the equation in standard form, p(x) can be. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e.
Solved 1. Integrating Factor. Find the general solution to
After writing the equation in standard form, p(x) can be. Can be solved using the integrating factor method. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e.
Integrating Factor Differential Equation All in one Photos
After writing the equation in standard form, p(x) can be. Can be solved using the integrating factor method. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. A linear first order o.d.e.
After Writing The Equation In Standard Form, P(X) Can Be.
A linear first order o.d.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Can be solved using the integrating factor method.