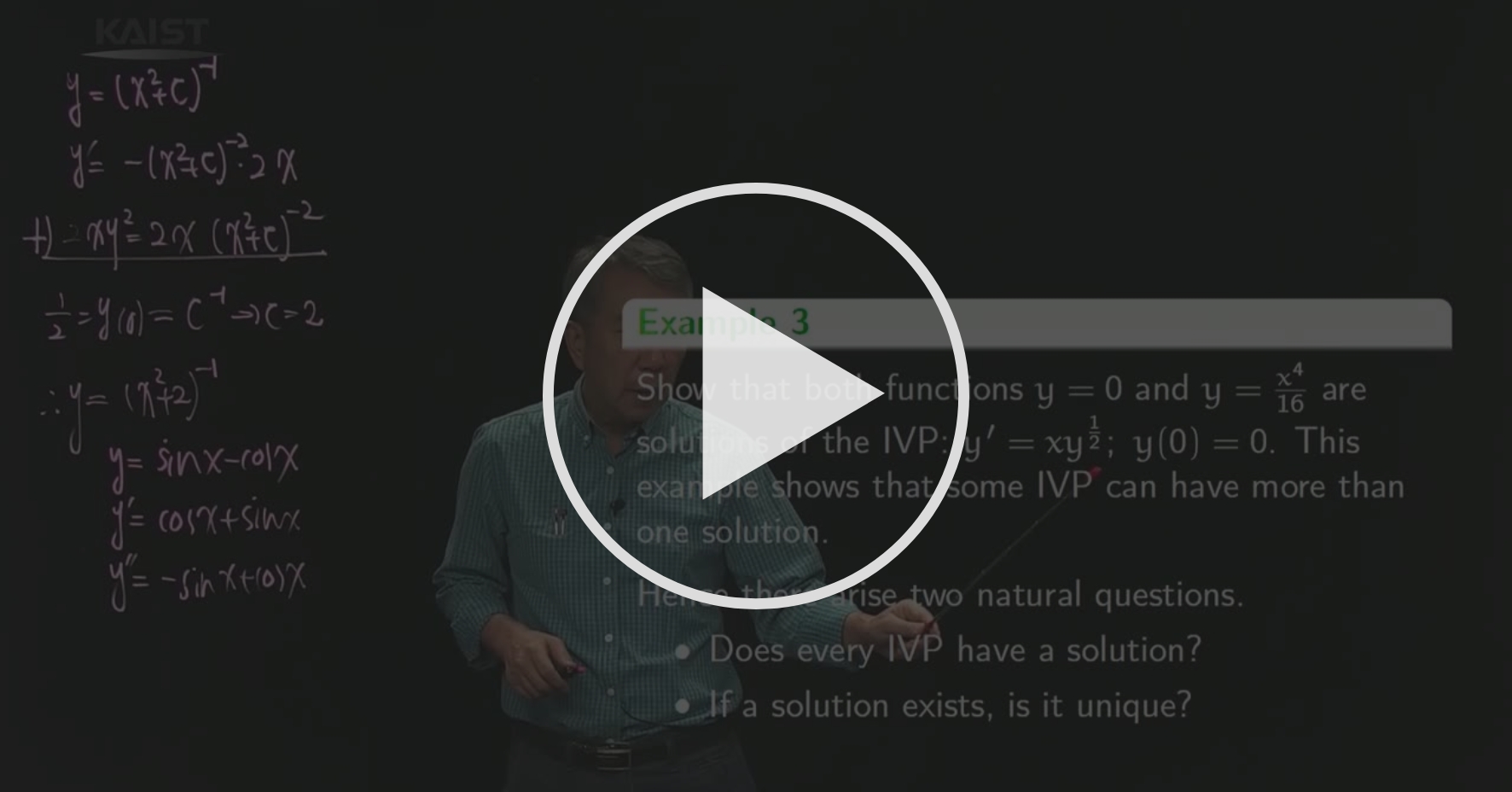
Picard's Theorem Differential Equations - |x − a| ≤ h, the first order ordinary differential equation: Has one and only one solution y = y(x) for which b = y(a). Y0(t 0 + a) =. If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Notes on the existence and uniqueness theorem for first order differential equations i.
Notes on the existence and uniqueness theorem for first order differential equations i. |x − a| ≤ h, the first order ordinary differential equation: Y0(t 0 + a) =. If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Has one and only one solution y = y(x) for which b = y(a).
Has one and only one solution y = y(x) for which b = y(a). |x − a| ≤ h, the first order ordinary differential equation: Y0(t 0 + a) =. If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Notes on the existence and uniqueness theorem for first order differential equations i.
Solved Differential equations. Please explain how Picard's
If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Y0(t 0 + a) =. Notes on the existence and uniqueness theorem for first order differential equations i. Has one and only one solution y = y(x) for which b = y(a). |x − a| ≤ h, the first order ordinary.
PPT Picard’s Method For Solving Differential Equations PowerPoint
Notes on the existence and uniqueness theorem for first order differential equations i. |x − a| ≤ h, the first order ordinary differential equation: Y0(t 0 + a) =. If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Has one and only one solution y = y(x) for which b.
18 Picard’s Theorem I Introduction Coursera
If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Y0(t 0 + a) =. Has one and only one solution y = y(x) for which b = y(a). Notes on the existence and uniqueness theorem for first order differential equations i. |x − a| ≤ h, the first order ordinary.
Picard’s Theorem Numerical Methods for Partial Differential Equations
Has one and only one solution y = y(x) for which b = y(a). |x − a| ≤ h, the first order ordinary differential equation: Y0(t 0 + a) =. If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Notes on the existence and uniqueness theorem for first order differential.
PPT Picard’s Method For Solving Differential Equations PowerPoint
Y0(t 0 + a) =. Has one and only one solution y = y(x) for which b = y(a). |x − a| ≤ h, the first order ordinary differential equation: Notes on the existence and uniqueness theorem for first order differential equations i. If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation.
(PDF) Evolutionary Equations, Picard's Theorem for Partial Differential
Notes on the existence and uniqueness theorem for first order differential equations i. If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Has one and only one solution y = y(x) for which b = y(a). Y0(t 0 + a) =. |x − a| ≤ h, the first order ordinary.
A Detailed Explanation of Picard's Theorem for Solving Differential
If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Y0(t 0 + a) =. |x − a| ≤ h, the first order ordinary differential equation: Has one and only one solution y = y(x) for which b = y(a). Notes on the existence and uniqueness theorem for first order differential.
PPT Picard’s Method For Solving Differential Equations PowerPoint
If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). |x − a| ≤ h, the first order ordinary differential equation: Has one and only one solution y = y(x) for which b = y(a). Y0(t 0 + a) =. Notes on the existence and uniqueness theorem for first order differential.
PPT Picard’s Method For Solving Differential Equations PowerPoint
Has one and only one solution y = y(x) for which b = y(a). Y0(t 0 + a) =. |x − a| ≤ h, the first order ordinary differential equation: Notes on the existence and uniqueness theorem for first order differential equations i. If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation.
PPT Picard’s Method For Solving Differential Equations PowerPoint
Y0(t 0 + a) =. Has one and only one solution y = y(x) for which b = y(a). |x − a| ≤ h, the first order ordinary differential equation: If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Notes on the existence and uniqueness theorem for first order differential.
|X − A| ≤ H, The First Order Ordinary Differential Equation:
Notes on the existence and uniqueness theorem for first order differential equations i. Has one and only one solution y = y(x) for which b = y(a). If the function f(x;y) satisfy the existence and uniqueness theorem for ivp (1), then the succesive approximation y n(x). Y0(t 0 + a) =.